Exercise 1.2

Exercise 1.2

1. Fill in the blanks

(i) The HCF of 45 and 75 is 15.

(ii) The HCF of two successive even numbers is 2.

(iii) If the LCM of 3 and 9 is 9, then their HCF is 3.

(iv) The LCM of 26, 39 and 52 is 156.

(v) The least number that should be added to 57 so that the sum is exactly divisible  by 2,3, 4 and 5 is 3.

2. Say True or False

(i) The numbers 57 and 69 are co-primes. [False]

(Common factor of 57 and 69 is 3)

(ii) The HCF of 17 and 18 is 1. [True]

(iii) The LCM of two successive numbers is the product of the numbers. [True]

(iv) The LCM of two co-primes is the sum of the numbers. [False]

(Product of two co−primes)

(v) The HCF of two numbers is always a factor of their LCM . [True]

3. Find the HCF of each set of numbers using prime factorisation method.

(i) 18,24 (ii) 51,85 (iii) 61,76 (iv) 84,120 (v) 27,45,81 (vi) 45,55,95

(i) 18, 24

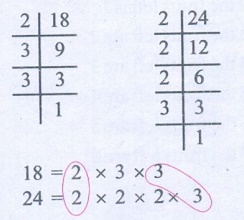
Product of common factors = 2 × 3 = 6

H.C.F. of 18 and 24 is 6

(ii) 51, 85

Common factors = 17

H.C.F. of 15 and 85 is 17

(iii) 61, 76

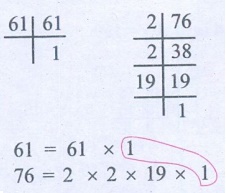
Common factors is 1

H.C.F. of 61 and 76 is 1

(iv) 84, 120

Product of common factors = 2 × 2 × 3 = 12

H.C.F. of 84 and 120 is 12

(v) 27, 45, 81

Product of common factors = 3 × 3 = 9

H.C.F. of  27, 45 and 81 is 9

(vi) 45, 55, 95

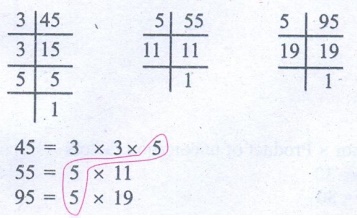
Common factor = 5

H.C.F. of 45, 55 and 95 = 5

4. Find the LCM of each set of numbers using prime factorisation method.

(i) 6,9 (ii) 8,12 (iii) 10,15 (iv) 14,42 (v) 30,40,60 (vi) 15,25,75

(i) 6, 9

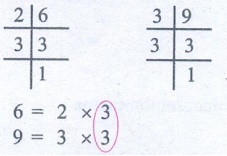
L.C.M. = Common factor × Product of uncommon factors

= 3 × (2 × 3) = 18

L.C.M. of 6 and 9 is 18

(ii) 8, 12

L.C.M. = Product of common factors × Product of uncommon factors

= (2 × 2) × (2 × 3) = 24

L.C.M. of 8 and 12 = 24

(iii) 10, 15

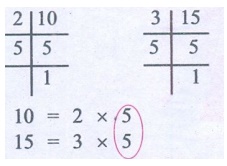
L.C.M. = Common factor × Product of uncommon factors

= 5 × (2 × 3) = 30

L.C.M. of 10 and 15 = 30

(iv) 14, 42

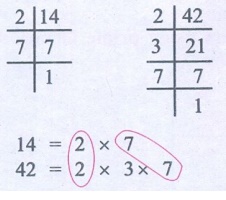
L.C.M. = Product of common factor × uncommon factor

= (2 × 7) × 3 = 42

L.C.M. of 14 and 42 = 42 

(v) 30, 40, 60

L.C.M. = Product of common factors of all the three numbers × common factors of two numbers × Uncommon factor

= (2 × 5) × (2 × 3) × 2 = 120

L.C.M. of 30, 40 and 60 = 120

(vi) 15, 25, 75

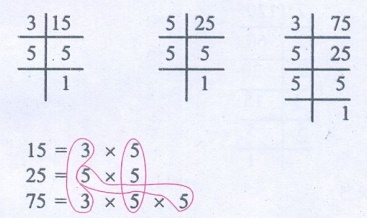
L.C.M. = Product of common factors of all the three numbers × product of common factors of two numbers

= 5 × (5 × 3) = 75

L.C.M. of 15, 25 and 75 = 75

5. Find the HCF and the LCM of the numbers 154, 198 and 286.

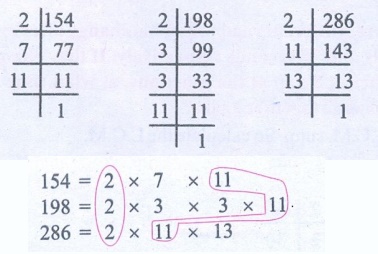
H.C.F. = Product of common factors of all the three numbers

= 2 × 11 = 22

L.C.M. = Product of common factors of all the three numbers × Product of uncommon factors = (2 × 11) × 7 × 3 × 3 × 13 = 18018

H.C.F. of 154,198 and 286 is 22

L.C.M. of 154,198 and 286 is 18018

6. What is the greatest possible volume of a vessel that can be used to measure exactly the volume of milk in cans (in full capacity) of 80 litres, 100 litres and 120 litres?

Solve the problem by using H.C.F.

H.C.F.of 80, 100 and 120 is 2 × 2 × 5 = 20

The greatest possible volume of a vessel that can be used to measure exactly the volume of milk in cans = 20 litres

7. The traffic lights at three different road functions change after every 40 seconds, 60 seconds and 72 seconds respectively. If they changed simultaneously together at 8 a.m at the unctions, at what time will they simultaneously change together again?

This sum is related to L.C.M. sum. So calculate the L.C.M.

L.C.M. of 40, 60 and 72 = 2 × 2 × 2  × 5 × 3 × 3

= 360 seconds

= 6 × 60 seconds = 6 minutes

All the three traffic lights change together again after 360 seconds

(6 minutes)

At 8.06 a.m the three traffic lights change together again.

8. The LCM of two numbers is 210 and their HCF is 14. How many such pairs are possible?

The L.C.M of two numbers =210

H.C.F = 14

Possible pairs = 2

They are 210, 14

70, 42

9. The LCM of two numbers is 6 times their HCF. If the HCF is 12 and one of the numbers is 36, then find the other number.

H.C.F of two numbers = 12

L.C.M. = 6 times their H.C.F

= 6 × 12 = 72

One of the numbers = 36

Product of two numbers = Product of H.C.F. × L.C.M.

36 × the other number = 12 × 72

The other number = [12 × 72] / 36 = 24

The other number = 24.

Objective Type Questions

10. Which of the following pairs is co-prime?

a) 51, 63

b) 52, 91

c) 71, 81

d) 81, 99

Answer: c) 71, 81

11. The greatest 4 digit number which is exactly divisible by 8, 9 and 12 is

a) 9999

b) 9996

c) 9696

d) 9936

Answer: d) 9936

12. The HCF of two numbers is 2 and their LCM is 154. If the difference between the numbers is 8, then the sum is

a) 26

b) 36

c) 46

d) 56

Answer: b) 36

13. Which of the following cannot be the HCF of two numbers whose LCM is 120

a) 60

b) 40

c) 80

d) 30

Answer: c) 80

ANSWERS:

Exercise 1.2

1. i) 15 ii) 2 iii) 3 iv) 156 v) 3

2. i) False ii) True iii) True iv) False v) True

3. i) 6 ii) 17 iii) 1 iv) 12  v) 9 vi) 5

4. i) 18 ii) 24 iii) 30 iv) 42 v) 120 vi) 75

5. HCF → 22; LCM → 18018

6. HCF = 20 litres

7. After 360 seconds (6 min), at 8.06 a.m

8. 2 pairs possible

9. 24

Objective Type Questions

10. c) 71, 81 11. d) 9936

12. b) 36

13. c) 80