Application Problems on HCF and LCM

Application Problems on HCF and LCM

Let us see the word problems that involve the HCF and the LCM concepts in daily life situations.

Example 6:

What is the greatest number that will divide 62, 78 and 109 leaving remainders 2, 3 and 4 respectively?

Solution: Get all the common factors of 62 − 2, 78 − 3 and 109 − 4, i.e., 60, 75 and 105 and see that the common factors will divide them all. The greatest number is the H.C.F of 60, 75 and 105.

60 = 2 × 2 × 3 × 5

75 = 3 × 5 × 5

105 = 3 × 5 × 7

Hence, the HCF is 3 × 5=15, which is the greatest number that will divide 62, 78, 109 leaving remainders 2, 3 and 4 respectively.

Example 7:

A book seller has 175 English books, 245 Science books and 385 Mathematics books. He wants to sell the books in a box, subject-wise in equal numbers. what will be the greatest number of the boxes required? Also find the number of books for each subject in a box.

Solution: This is a HCF related problem. So, we need to find the HCF of 175, 245 and 385.

The HCF of 175, 245 and 385 is the product of the common factors 5 and 7 i.e, 5 × 7=35

Since each box contains equal number of books, the greatest possible number of boxes = 35

The number of English books in each box = 175÷35=5

The number of Science books in each box = 245÷35=7

The number of Maths books in each box = 385÷35=11

Hence, the total number of books in each box is 5+7+11=23.

Note

* LCM is always greater than or equal to the largest of the given numbers.

* LCM will always be a multiple of HCF.

Example 8:

Find the ratio of the HCF and the LCM of the numbers 18 and 30.

Solution: Now, 18 = 2 × 3 × 3 and 30 = 2 × 3 × 5 and their HCF is 2 × 3 = 6 and LCM is 2 × 3 × 3 × 5 = 90

Hence, HCF : LCM = 6:90 = 1:15

Example 9:

Find the smallest number that can be divided by 254 and 508 which leaves the remainder 4.

Solution: All common multiples of 254 and 508 will be divisible by both the numbers. Let us find the LCM of 254 and 508 (by division method).

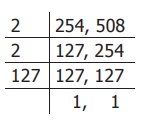
LCM of 254, 508 = 2 × 2 × 127 = 508

Thus, 508 is the smallest common number that is divisible by 254 and 508.  Now, as we need remainder 4 while dividing, the required number is 4 more than the LCM and so, the required number is 508 + 4 =512.

Example 10:

What is the smallest 5 digit number that is exactly divisible by 72 and 108?

Solution: First let us find the LCM of 72 and 108 (by division method).

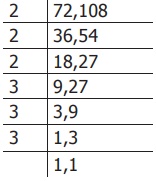
LCM of 72 and 108= 2 × 2 × 2 × 3 × 3 × 3 = 216

Now, all multiples of 216 will also be common multiples of 72 and 108.

The smallest 5 digit number = 10,000.

Now, 10,000 ÷ 216 gives quotient as 46 and remainder as 164.

Hence the next multiple of 216 i.e., 216 × 47 = 10,152 is the required smallest 5 digit number that is exactly divisible by 72 and 108.

Example 11:

There are four Mobile Phones in a house. At 5 a.m, all the four Mobile Phones will ring together. Thereafter, the first one rings every 15 minutes, the second one rings every 20 minutes, the third one rings every 25 minutes and the fourth one rings every 30 minutes. At what time, will the four Mobile Phones ring together again?

Solution: This is a LCM related sum. So, we need to find the LCM of 15, 20, 25 and 30.

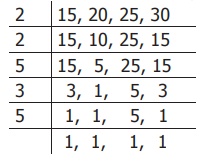
The LCM of 15, 20, 25 and 30 is 2 × 2 × 3 × 5 × 5 = 300 minutes = 5 × 60 minutes = 5 × 1 hour = 5 hours

Thus, the four Mobile Phones will ring together again at 10.00 a.m.

Try this

A small boy went to a town to sell a basket of wood apples. On the way, some robbers grabbed the fruits from him and ate them. The small boy went to the King and complained. The King asked him, “How many wood apples did you bring ?”. The boy replied, “Your Majesty! I didn’t know, but I knew that if you divided my fruits into groups of 2, one fruit would be left in the basket”. He continued saying that if the fruits were divided into groups of 3, 4, 5 and 6, the fruits left in the basket would be 2, 3, 4 and 5 respectively. Also, if the fruits were divided into groups of 7, no fruit would be there in the basket. Can you find the number of fruits, the small boy had initially ?

(This problem is taken from the famous Mathematics problems collection book in Tamil called “Kanakkathikaram” under the heading of “Wood Apple Problem”)

If the fruits were divided into group of 2 the fruits left is 1

If the fruits were divided into group of 3 the fruits left are 2

If the fruits were divided into group of 4 the fruits left are 3

If the fruits were divided into group of 5 the fruits left are 4

If the fruits were divided into group of 6 the fruits left are 5

If the fruits were divided into group of 7 the fruits left are 0

L.C.M = l × 2 × 3 × 4 × 5 = 120

It is divisible by 7.

∴ 120/7 = 17 remainder 1

The number divisible by 7 is 119.

The number of fruits the small boy had initially = 119