Polynomials

Polynomials

The following dot diagrams show the sequence of patterns.

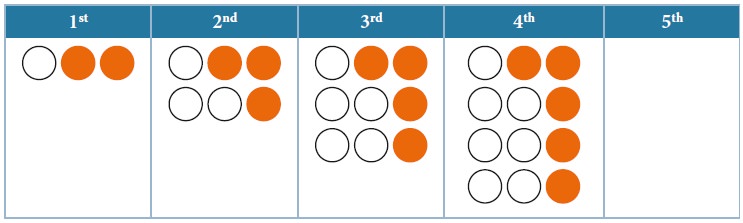
(a) Draw the fifth pattern in the sequence in the space above.

(b) How many dots of each colour will be there in the 10th pattern?

White: ____________ Colour : ____________

(c) The number of colour dots in the nth diagram is given by the expression ____________

(d) Write algebraic expressions for the number of white dots and for the total number of dots.

Solution:

(a) Draw the fifth pattern in the sequence in the space above.

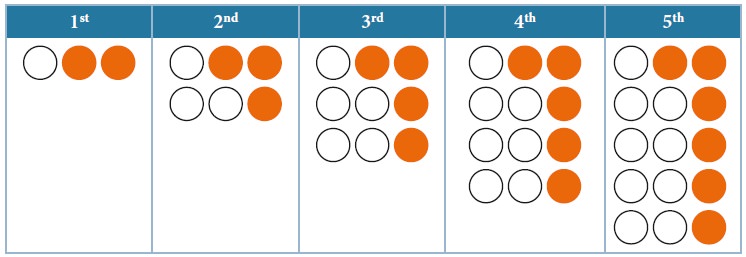
(b) How many dots of each colour will be there in the 10th pattern?

White: 19 Colour : 11

(c) The number of colour dots in the nth diagram is given by the expression n+1

(d) Write algebraic expressions for the number of white dots and for the total number of dots.

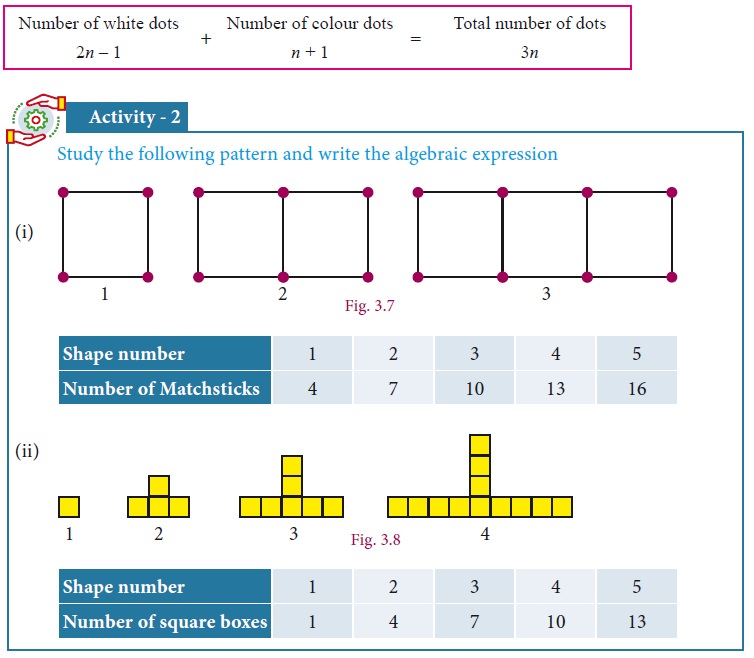
1. Polynomial in One Variable

An algebraic expression of the form p(x)= a_nxⁿ + a_n-1x^n-1 +…….+ a₂x² + a₁ + a₀ is called Polynomial in one variable x of degree ‘n’ where a₀, a₁, a₂,... a_n are constants (a_n ≠ 0) and n is a whole number.

In general polynomials are denoted by f(x) g(x) p(t) q(z) and r(x) and so on.

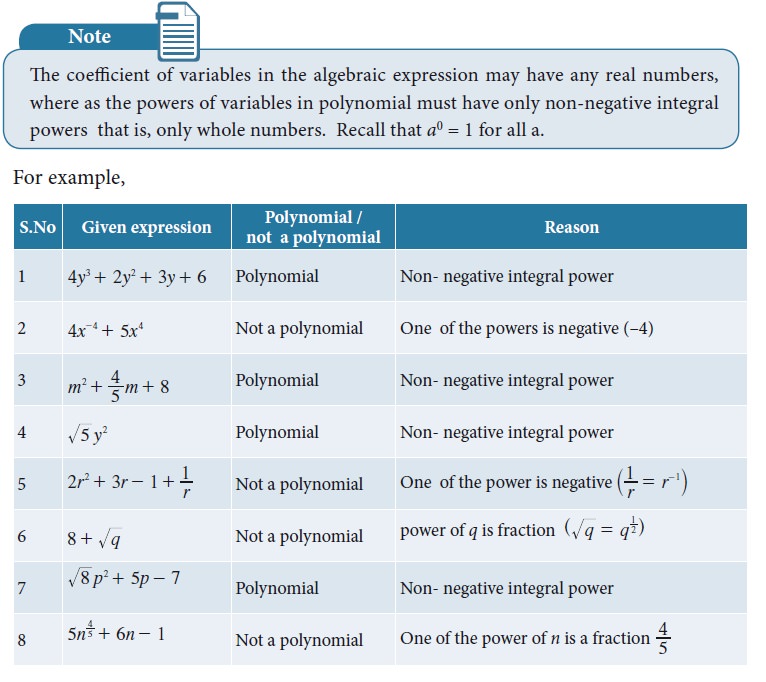
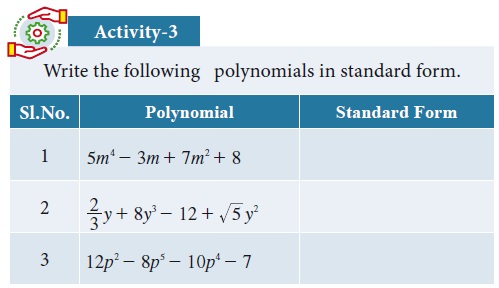
2. Standard Form of a Polynomial

We can write a polynomial p(x) in the decreasing or increasing order of the powers of x. This way of writing the polynomial is called the standard form of a polynomial.

For example

(i) 8x⁴+ 4x³ -7x² -9x + 6  

(ii) 5 – 3y + 6y² + 4y³ – y⁴

3. Degree of the Polynomial

In a polynomial of one variable, the highest power of the variable is called the degree of the polynomial.

In case of a polynomial of more than one variable, the sum of the powers of the variables in each term is considered and the highest sum so obtained is called the degree of the polynomial.

This is intended as the most significant power of the polynomial. Obviously when we write x²+5x the value of x² becomes much larger than 5x for large values of x. So we could think of x² + 5x being almost the same as x² for large values of x. So the higher the power, the more it dominates. That is why we use the highest power as important information about the polynomial and give it a name.

Example 3.1

Find the degree of each term for the following polynomial and also find the degree of the polynomial

6ab⁸ + 5a ² b³ c ² - 7ab + 4b² c + 2

Solution

Given 6ab⁸ + 5a²b³c²-7ab+4b²c+2

Degree of each of the terms is given below.

6ab⁸ has degree (1+8) = 9

5a²b³c² has degree (2+3+2) = 7

7ab has degree (1+1) = 2

4b²c has degree (2+1) = 3

The constant term 2 is always regarded as having degree Zero.

The degree of the polynomial6ab⁸ + 5a²b³c²-7ab+4b²c+2.

 = the largest exponent in the polynomial

 = 9

4. A very Special Polynomial

We have said that coefficients can be any real numbers. What if the coefficient is zero? Well that term becomes zero, so we won’t write it. What if all the coefficients are zero? We acknowledge that it exists and give it a name.

It is the polynomial having all its coefficients to be Zero.

g (t) = 0t ⁴ + 0t² - 0t ,      h (p) = 0p ² - 0p + 0

From the above example we see that we cannot talk of the degree of the Zero polynomial, since the above two have different degrees but both are Zero polynomial. So we say that the degree of the Zero polynomial is not defined

The degree of the Zero polynomial is not defined

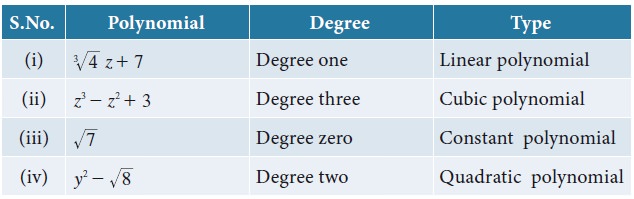
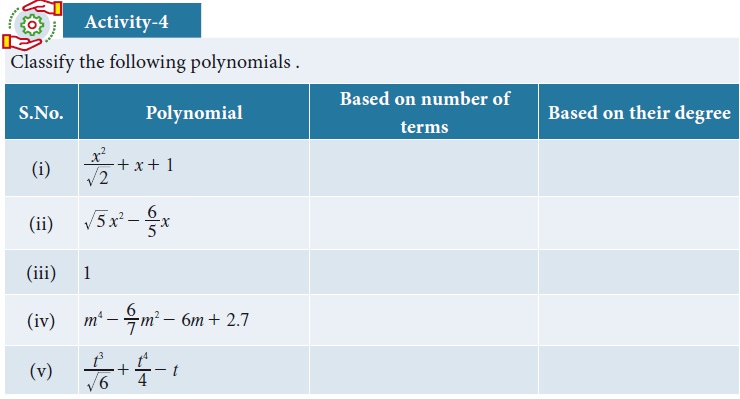
5. Types of Polynomials

Example 3.2

Classify the following polynomials based on number of terms.

Example 3.3

Classify the following polynomials based on their degree.