Arithmetic of Polynomials

Arithmetic of Polynomials

We now have a rich language of polynomials, and we have seen that they can be classified in many ways as well. Now, what can we do with polynomials? Consider a polynomial on x.

We can evaluate the polynomial at a particular value of x. We can ask how the function given by the polynomial changes as x varies. Write the polynomial equation p(x) = 0 and solve for x. All this is interesting, and we will be doing plenty of all this as we go along. But there is something else we can do with polynomials, and that is to treat them like numbers! We already have a clue to this at the beginning of the chapter when we saw that every positive integer could be represented as a polynomial.

Following arithmetic, we can try to add polynomials, subtract one from another, multiply polynomials, divide one by another. As it turns out, the analogy between numbers and polynomials runs deep, with many interesting properties relating them. For now, it is fun to simply try and define these operations on polynomials and work with them.

1. Addition of Polynomials

The addition of two polynomials is also a polynomial.

Example 3.4

Let p(x) = 4x² - 3x+2x³+5 and q(x)=x²+2x+4 find p(x)+q(x)

Solution

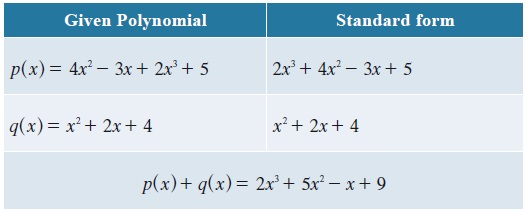
We see that p(x) + q(x) is also a polynomial. Hence the sum of any two polynomialsis also a polynomial.

2. Subtraction of Polynomials

The subtraction of two polynomials is also a polynomial.

Example 3.5

Let p(x) = 4x²-3x+2x³+5 and q(x)=x²+2x+4 find p(x)-q(x)

Solution

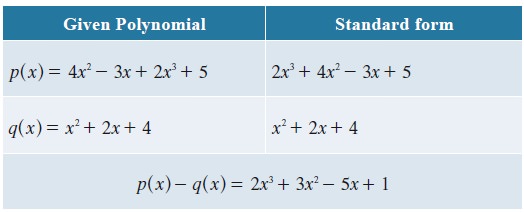
We see that p(x) – q(x) is also a polynomial. Hence the subtraction of any two polynomials is also a polynomial.

3. Multiplication of Two Polynomials

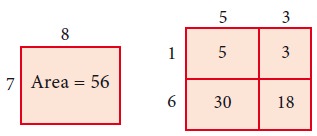
Divide a rectangle with 8 units of length and 7 units of breadth into 4 rectangles as shown below, and observe that the area is same, this motivates us to study the multiplication of polynomials.

For example, considering length as (x+1) and breadth as (3x+2) the area of the rectangle can be found by the following way.

Example 3.6

Find the product (4x – 5) and (2x² + 3x – 6).

Solution

To multiply (4x – 5) and (2x² + 3x – 6) distribute each term of the first polynomial to every term of the second polynomial. In this case, we need to distribute the terms 4x and –5. Then gather the like terms and combine them: