Division of Polynomials

Division of Polynomials

Let us consider the numbers 13 and 5. When 13 is divided by 5 what is the quotient and remainder.?

Yes, of course, the quotient is 2 and the remainder is3.We write 13 = (5×2)+3

Let us try.

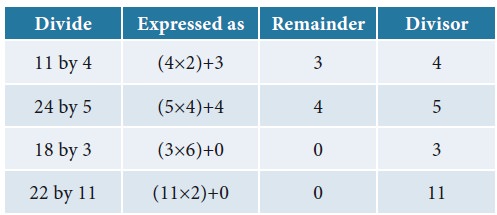
From the above examples, we observe that the remainder is less than the divisor.

Can we say ? that when the remainder is 0, then the dividend is the multiple of the divisor?

Dividend = ( Divisor × Quotient ) + Remainder.

Is it possible to divide one polynomial by another ?

Of course, yes, and the way to do it is just the way similar to what you do with numbers!

Let us start with the division of a polynomial by a monomial.

Example 3.11

Divide x³ -4x² + 6x by x, where , x ≠ 0

Solution

We have

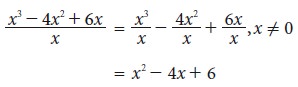
1. Division Algorithm for Polynomials

Let p(x) and g(x) be two polynomials such that degree of p(x) ≥degree of g(x) and g(x) ≠ 0. Then there exists unique polynomials q(x) and r(x) such that

p(x) = g (x) x q(x) + r(x)  … (1)

where r(x) = 0 or degree of r(x) < degree of g(x).

The polynomial p(x) is the Dividend, g(x) is the Divisor, q(x) is the Quotient and r(x)  is the Remainder. Now (1) can be written as

 Dividend = ( Divisor × Quotient ) + Remainder.

If r(x) is zero, then we say p(x) is a multiple of g(x). In other  words, g(x) divides p(x).

If it looks complicated, don’t worry ! it is important to know how to divide polynomials, and that comes easily with practice. The examples below will help you.

Example 3.12

Find the quotient and the remainder when (5x²-7x+2) / (x-1)

Solution

Example 3.13

Find quotient and the remainder when f(x) is divided by g(x)

(i) f(x) = (8x³–6x²+15x–7), g(x) = 2x+1.  (ii) f(x) = x³ + 1, g(x) = x+1

Solution

Example 3.14

If x⁴ –3x³ + 5x² –7 is divided by x² + x + 1 then find the quotient and the remainder.

Solution