Physical Principles of Optics - Eye

Physical Principles of Optics

Before it is possible to understand the optical system of the eye, the student must first be thor-oughly familiar with the basic principles of optics, including the physics of light refraction, focusing, depth of focus, and so forth. A brief review of these physical principles is presented; then the optics of the eye is discussed.

Refraction of Light

Refractive Index of a Transparent Substance. Light rays travel through air at a velocity ofabout 300,000 km/sec, but they travel much slower through transparent solids and liquids. The refractive index of a transparent substance is the ratio of the velocity of light in air to the velocity in the substance. The refractive index of air itself is 1.00. Thus, if light travels through a particular type of glass at a velocity of 200,000 km/sec, the refractive index of this glass is 300,000 divided by 200,000, or 1.50.

Refraction of Light Rays at an Interface Between Two Media with Different Refractive Indices.

When light rays traveling forward in a beam (as shown in Figure 49–1A) strike an interface that is perpendicular to the beam, the rays enter the second medium without deviating from their course. The only effect that occurs is decreased veloc-ity of transmission and shorter wavelength, as shown in the figure by the shorter distances between wave fronts.

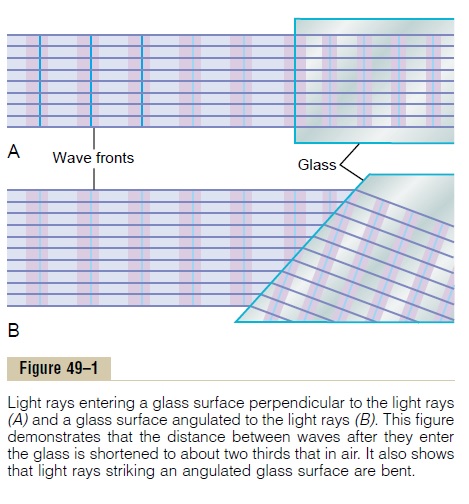
       If the light rays pass through an angulated interface as shown in Figure 49–1B, the rays bend if the refractive indices of the two media are different from each other. In this particular figure, the light rays are leaving air, which has a refractive index of 1.00, and are entering a block of glass having a refractive index of 1.50. When the beam first strikes the angulated interface, the lower edge of the beam enters the glass ahead of the upper edge. The wave front in the upper portion of the beam con-tinues to travel at a velocity of 300,000 km/sec, while that which entered the glass travels at a velocity of 200,000 km/sec. This causes the upper portion of the wave front to move ahead of the lower portion, so that the wave front is no longer ver-tical but angulated to the right. Because the direction in which light travels is alwaysperpendicular to the plane of the wave front, the direction of travel of the light beambends downward.

       This bending of light rays at an angulated interface is known as refraction. Note particularly that the degree of refraction increases as a function of (1) the ratio of the two refractive indices of the two transparent media and (2) the degree of angu-lation between the interface and the entering wave front.

Application of Refractive Principles to Lenses

Convex Lens Focuses Light Rays. Figure 49–2 shows parallel light rays entering a convexlens. The light rays passing through the center of the lens strike the lens exactly per-pendicular to the lens surface and, therefore, pass through the lens without being refracted. Toward either edge of the lens, however, the light rays strike a progres-sively more angulated interface. The outer rays bend more and more toward the center, which is called convergence of the rays. Half the bending occurs when the rays enter the lens, and half as they exit from the opposite side. (At this time, the student should pause and analyze why the rays bend toward the center on leaving the lens.) Finally, if the lens has exactly the proper curvature, parallel light

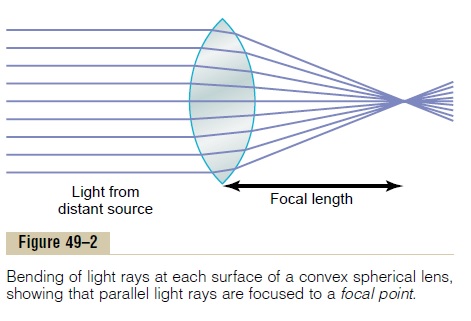
rays passing through each part of the lens will be bent exactly enough so that all the rays will pass through a single point, which is called the focal point.

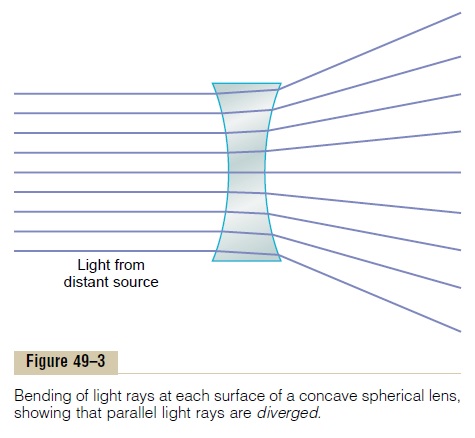
Concave Lens Diverges Light Rays. Figure 49–3 shows theeffect of a concave lens on parallel light rays. The rays that enter the center of the lens strike an interface that is perpendicular to the beam and, therefore, do not refract. The rays at the edge of the lens enter the lens ahead of the rays in the center. This is opposite to the effect in the convex lens, and it causes the peripheral light rays to diverge from the light rays that pass through the center of the lens. Thus, the concave lens diverges light rays, but the convex lens converges light rays.

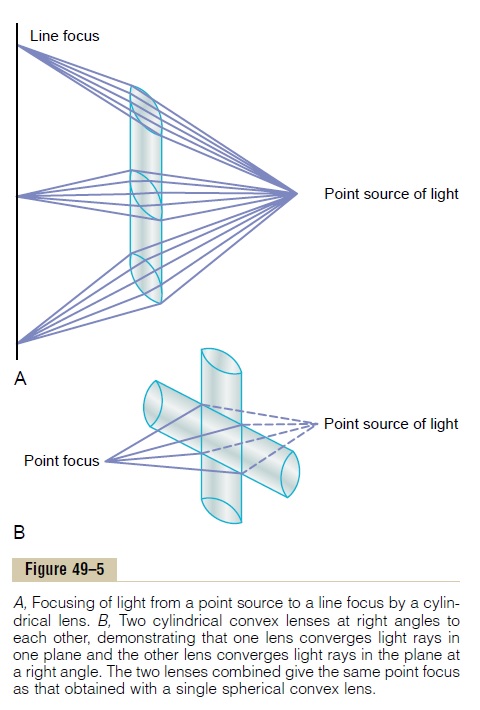
Cylindrical Lens Bends Light Rays in Only One Plane—Comparison with Spherical Lenses. Figure 49–4 shows both a convexspherical lens and a convex cylindrical lens. Note thatthe cylindrical lens bends light rays from the two sides of the lens but not from the top or the bottom. That is, bending occurs in one plane but not the other.Thus, par-allel light rays are bent to a focal line. Conversely, light rays that pass through the spherical lens are refracted at all edges of the lens (in both planes) toward the central ray, and all the rays come to a focal point.

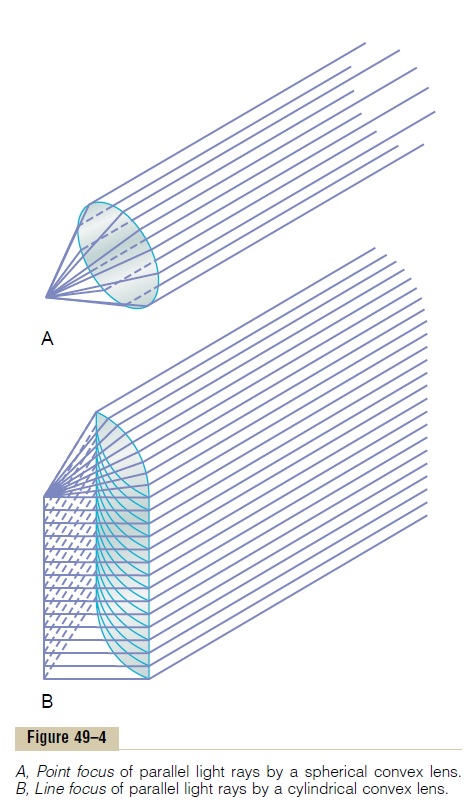
The cylindrical lens is well demonstrated by a test tube full of water. If the test tube is placed in a beam of sunlight and a piece of paper is brought progressively closer to the opposite side of the tube, a certain distance will be found at which the light rays come to a focal line. The spherical lens is demonstrated by an ordinary mag-nifying glass. If such a lens is placed in a beam of sun-light and a piece of paper is brought progressively closer to the lens, the light rays will impinge on a common focal point at an appropriate distance.

Concave cylindrical lenses diverge light rays in onlyone plane in the same manner that convex cylindrical lenses converge light rays in one plane.

Combination of Two Cylindrical Lenses at Right Angles Equals a Spherical Lens. Figure 49–5B shows twoconvex cylindrical lenses at right angles to each other. The vertical cylindrical lens converges the light rays that pass through the two sides of the lens, and the horizon-tal lens converges the top and bottom rays. Thus, all the light rays come to a single-point focus. In other words, two cylindrical lenses crossed at right angles to each other perform the same function as one spherical lens of the same refractive power.

Focal Length of a Lens

The distance beyond a convex lens at which parallel rays converge to a common focal point is called the focallength of the lens. The diagram at the top of Figure 49–6demonstrates this focusing of parallel light rays.

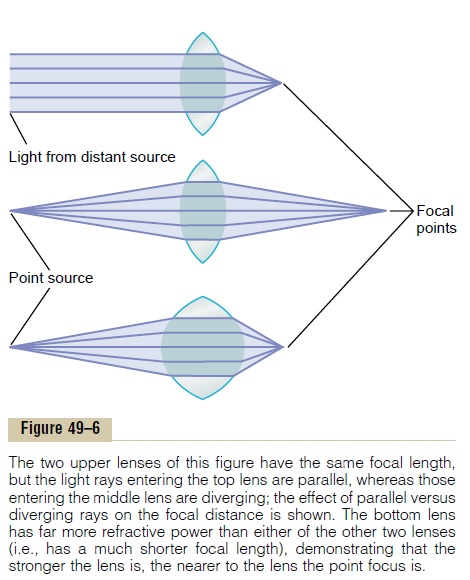
In the middle diagram, the light rays that enter the convex lens are not parallel but are diverging because the origin of the light is a point source not far away from the lens itself. Because these rays are diverging outward from the point source, it can be seen from the diagram that they do not focus at the same distance away from the lens as do parallel rays. In other words, when rays of light that are already diverging enter a convex lens, the distance of focus on the other side of the lens is farther from the lens than is the focal length of the lens for parallel rays.

The bottom diagram of Figure 49–6 shows light rays that are diverging toward a convex lens that has far greater curvature than that of the other two lenses in the figure. In this diagram, the distance from the lens at which the light rays come to focus is exactly the same as that from the lens in the first diagram, in which the lens is less convex but the rays entering it are parallel. This demonstrates that both parallel rays and diverging rays can be focused at the same distance beyond a lens, provided the lens changes its convexity.

The relation of focal length of the lens, distance of the point source of light, and distance of focus is expressed by the following formula: in which f is the focal length of the lens for parallel rays, a is the distance of the point source of light from thelens, and b is the distance of focus on the other side of the lens.

Formation of an Image by a Convex Lens

Figure 49–7A shows a convex lens with two point sources of light to the left. Because light rays pass through the center of a convex lens without being refracted in either direction, the light rays from each point source of light are shown to come to a point focus on the opposite side of the lens directly in line with thepoint source and the center of the lens.

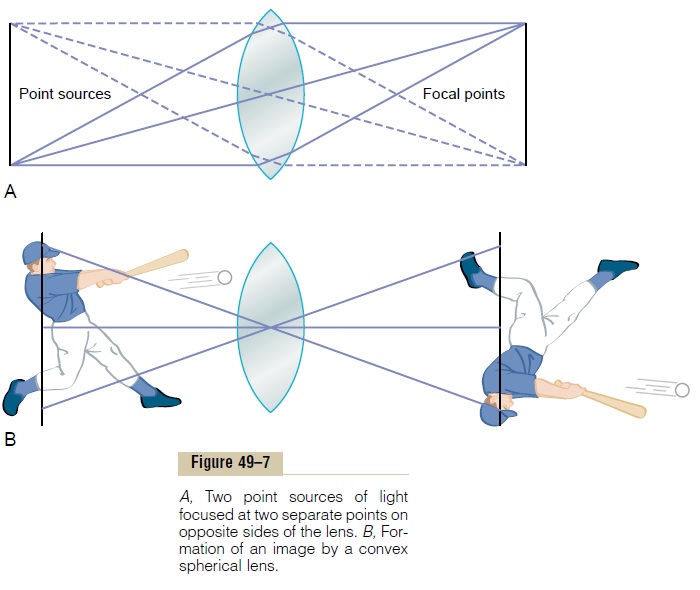
Any object in front of the lens is, in reality, a mosaic of point sources of light. Some of these points are very bright, some are very weak, and they vary in color. Each point source of light on the object comes to a separate point focus on the opposite side of the lens in line with the lens center. If a white sheet of paper is placed at the focus distance from the lens, one can see an image of the object, as demonstrated in Figure 49–7B. However, this image is upside down with respect to the original object, and the two lateral sides of the image are reversed. This is the method by which the lens of a camera focuses images on film.

Measurement of the Refractive Power of a Lens—“Diopter”

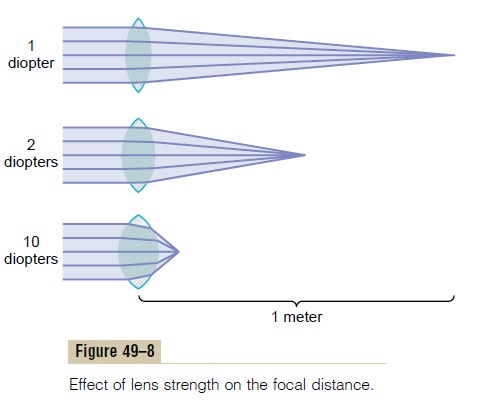
The more a lens bends light rays, the greater is its “refractive power.” This refractive power is measured in terms of diopters. The refractive power in diopters of a convex lens is equal to 1 meter divided by its focal length. Thus, a spherical lens that converges parallel light rays to a focal point 1 meter beyond the lens has a refractive power of +1 diopter, as shown in Figure 49–8. If the lens is capable of bending parallel light rays twice as much as a lens with a power of +1 diopter, it is said to have a strength of +2 diopters, and the light rays come to a focal point 0.5 meter beyond the lens. A lens capable of converging parallel light rays to a focal point only 10 centimeters (0.10 meter) beyond the lens has a refractive power of +10 diopters.

The refractive power of concave lenses cannot be stated in terms of the focal distance beyond the lens because the light rays diverge, rather than focus to a point. However, if a concave lens diverges light rays at the same rate that a 1-diopter convex lens converges them, the concave lens is said to have a dioptric strength of –1. Likewise, if the concave lens diverges light rays as much as a +10-diopter lens converges them, this lens is said to have a strength of –10 diopters.

Concave lenses “neutralize” the refractive power of convex lenses. Thus, placing a 1-diopter concave lens immediately in front of a 1-diopter convex lens results in a lens system with zero refractive power.

The strengths of cylindrical lenses are computed in the same manner as the strengths of spherical lenses, except that the axis of the cylindrical lens must be stated in addition to its strength. If a cylindrical lens focuses parallel light rays to a line focus 1 meter beyond the lens, it has a strength of +1 diopter. 

Conversely, if a cylin-drical lens of a concave type diverges light rays as much as a +1-diopter cylindrical lens converges them, it has a strength of –1 diopter. If the focused line is horizontal, its axis is said to be 0 degrees. If it is vertical, its axis is 90 degrees.