Perimeter and Area of Combined Shapes

Perimeter and Area of Combined Shapes

A Combined shape is the combination of several closed shapes. The perimeter is calculated by adding all the outer sides (boundaries) of the combined shape. The area is calculated by adding all the areas of closed shapes from which the combined shape is formed.

Example 12

Find the perimeter of the given figure.

Solution

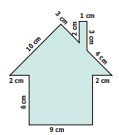
Perimeter = Total length of the boundary

                = (6 + 2 + 10 + 3 + 2 + 1 + 3 +  4 + 2 + 6 + 9) cm

               = 48 cm

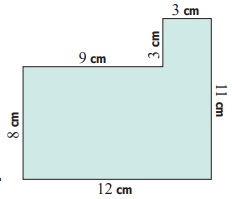
Example 13

Find the perimeter and the area of the following ‘L’ shaped figure.

Solution

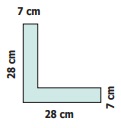
 Perimeter = (28 + 7 + 21 + 21 + 7 + 28) cm.

                  = 112 cm.

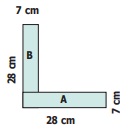
To find the area of the L shaped figure, it is divided into two rectangles A and B.

The area of the ‘L’ shaped figure = (196 + 147) sq. cm

                                                     = 343 sq. cm.

Activity

Find the area of the given ‘L’ shaped rectangular figure by dividing it into squares of equal sizes.

Think

Can you find the area of ‘L’ shaped figure as the difference between two areas.

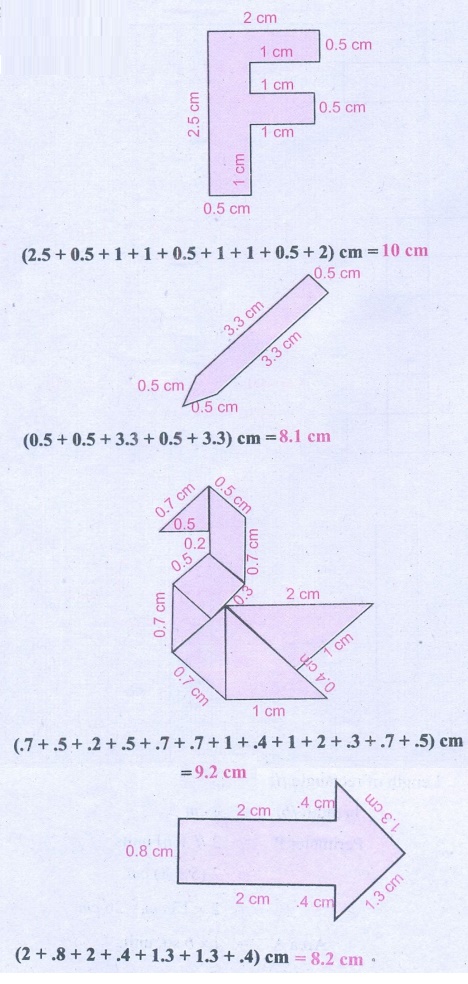
Try these

Measure using ruler and find the perimeter of each of the following diagram.

Activity

Form all possible shapes of perimeter 80 cm with 9 identical squares, each of side 4 cm.

1. Impact on Removing / Adding a portion from / to a given shape

Consider a rectangle of sides 8 cm and 12 cm.

Length, l = 12 cm; Breadth b = 8 cm.

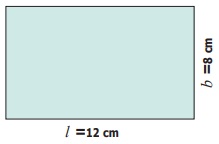
Area, A = (l × b) sq. units.

              = 12 × 8

              = 96 sq. cm.

Perimeter, P = 2 (l + b) units.

                  = 2 (12 + 8)

                   = 40 cm.

Find the area and perimeter of the rectangle in the following situations and observe the changes.

Situation 1

A square of side 3 cm is cut at a corner of the rectangle.

Area, A = (l × b) – (s × s) sq. units.

              = (12 × 8) – (3 × 3)

              = 87 sq. cm.

Perimeter, P = (Total boundary) units.

                    = 8+12+5+3+3+9 = 40 cm.

The perimeter is not changed. But the area is reduced.

Situation 2

A square of side 3 cm is attached to the rectangle.

Area, A = (l × b) + (s × s) sq. units.

              = (12 × 8) + (3 × 3)

               = 105 sq. cm.

Perimeter, P = (Total boundary) units.

                    = 8+12+11+3+3+9 = 46 cm.

Here both the perimeter and the area are increased.

Example 14

Four identical square floor mats of side 15 cm are joined together to form either a rectangular mat or a square mat. Which mat will have a larger area and a longer perimeter?

Solution

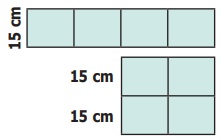
Perimeter of a rectangle, P = 2 (l + b) units.

                          = 2 (60+15) cm. = 150 cm.

Area of a rectangle, A = (l × b) sq. units.

                            = 60 × 15 = 900 sq. cm.

Perimeter of a square, P = (4 × s) units

                         = (4 × 30) cm = 120 cm

Area of a square, A = (s × s) sq. units.

                          = 30 × 30 = 900 sq. cm.

There is no change in their areas. But, the rectangular mat will have longer perimeter.

Activity

Cut a rectangular sheet along one of its diagonals. Two identical scalene right angled triangles are obtained. Join them along their sides of identical length in all possible ways. Six different shapes can be obtained. Four of them are given. Find the remaining two shapes. Find the perimeter of all the six shapes and fill in the table.

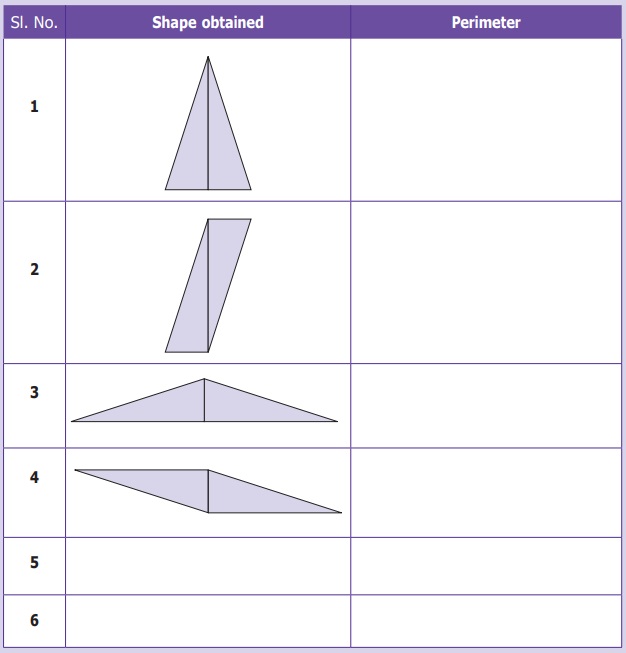
Based on the above activity answer the following questions:

i) Are the perimeters same for all the shapes?

ii) Which shape has the longest perimeter?

iii) Which shape has the shortest perimeter?

iv) Are the areas of all the shapes same? Why?

DO YOU KNOW?

• Shapes with the same perimeter may have different areas.

• Shapes with the same area may have different perimeters.