Exercise 3.2

Exercise 3.2

Miscellaneous Practice Problems

1. A piece of wire is 36 cm long. What will be the length of each side if we form

i) a square

ii) an equilateral triangle.

Length of a piece of wire = 36 cm

i) Perimeter of a square P = 4S = 36 cm

S = 36 / 4 = 9 cm

The length of each side of the square = 9 cm

ii) Perimeter of an equilateral triangle P = 3 a = 36 cm

S = 36 / 3 = 12 cm

The length of each side of the equilateral triangle = 12 cm

2. From one vertex of an equilateral triangle with side 40 cm, an equilateral triangle with 6 cm side is removed. What is the perimeter of the remaining portion?

The length of the side of the equilateral triangle a = 40 cm

Perimeter P = 3a = 3 × 40 = 120 cm

Removed side = 6 cm

The perimeter ofthe remaining portion = 114 cm

3. Rahim and Peter go for a morning walk, Rahim walks around a square path of side 50 m and Peter walks around a rectangular path with length 40 m and breadth 30 m. If both of them walk 2 rounds each, who covers more distance and by how much?

Rahim walks around a square path

The length of the side S = 50 m

Perimeter P = 4S = 4 × 50 = 200 m

2 rounds = 2 × 200 = 400 m 

Peter walks around a rectangle path

The length of the rectangle l = 40 m

Breadth b = 30 m

Perimeter P = 2 (l + b) units

= 2 (40 +30) m

= 2 × 70 = 140 m

2 rounds = 2 × 140 = 280 m

The distance covers by Rahim = 400 m (—)

The distance covers by Peter = 280 m

Rahim covers more distance = 120 m

Rahim covers more distance by 120 m.

4. The length of a rectangular park is 14 m more than its breadth. If the perimeter of the park is 200 m, what is its length? Find the area of the park.

Breadth of Rectangular path = b m

Length = b + 14 m

Perimeter P = 200 m

2 (l + b) = 200

2 (b + 14 + b) = 200

2b + 14 = 100

2b = 100 – 14 = 86

b = 43 m

Breadth b = 43 m

Length l = b + 14 = 43 + 14 m

= 57 m

Length of the park l = 57 m

Breadth b = 43 m 

Area A = l × b sq. units

= 57 × 43 sq.m

= 2451 sq. m

The area of the park = 2451 sq. m

5. Your garden is in the shape of a square of side 5 m. Each side is to be fenced with 2 rows of wire. Find how much amount is needed to fence the garden at ₹ 10 per metre.

Side of the square S = 5 m

Perimeter P = 4S = 4 × 5 = 20 m

2 rows = 2 × 20 = 40 m

Amount needed to fence 1 metre = ₹ 10

Amount needed to fence 40 metres = ₹10 × 40

= ₹ 400

Amount needed to fence the garden = ₹ 400

Challenge Problems

6. A closed shape has 20 equal sides and one of its sides is 3 cm. Find its perimeter.

One of the sides a = 3 cm

Total number of sides = 20

Perimeter of the closed shape of 20 equal sides

= 20 a = 20 × 3 = 60 cm

7. A rectangle has length 40 cm and breadth 20 cm. How many squares with side 10 cm can be formed from it.

Length of rectangle l = 40 cm

Breadth b = 20 cm

Area A = l × b sq. units 

= 40 × 20 = 800 sq.cm

Side of square S = 10 cm

Area A = S × S= 10 × 10 = 100 sq.cm

Number of squares formed = Area of rectangle / Area of square

= 800 / 100 = 8

Number of squares formed = 8.

8. The length of a rectangle is three times its breadth. If its perimeter is 64 cm, find the sides of the rectangle.

Let Breadth of rectangle = b cm

Length l = 3 b cm

Perimeter P = 2 (l + b) =  64 cm

2 (3b + b) = 64

2 × 4 b = 64

b = 64 / 8 = 8 cm

b = 8 cm

l = 3 b = 3 × 8 = 24 cm

Length of the rectangle = 24 cm

Breadth = 8 cm

9. How many different rectangles can be made with a 48 cm long string? Find the possible pairs of length and breadth of the rectangles.

Length of string = 48 cm

Perimeter of the rectangle P = 2 (l + b) = 48 cm 

l + b = 24 cm

1 + 23 = 24

2 + 22 = 24

3 + 21 = 24

4 + 20 = 24

5 + 19 = 24

6 + 18 = 24

7 + 17 = 24

8 + 16 = 24

9 + 15 = 24

10 + 14 = 24

11 + 13 = 24

12 + 12 = 24

12 different rectangles can be made with a 48 cm long string.

The possible pairs of length and breadth of the rectangles are.

(1, 23), (2, 22), (3, 21), (4, 20), (5, 19), (6, 18), (8, 17), (8, 16), (9, 15), (10, 14), (11, 13) and (12, 12).

10. Draw a square B whose side is twice of the square A. Calculate the perimeters of the squares A and B.

Let the side of the square A = 3 cm

Let the side of the square B = 6 cm

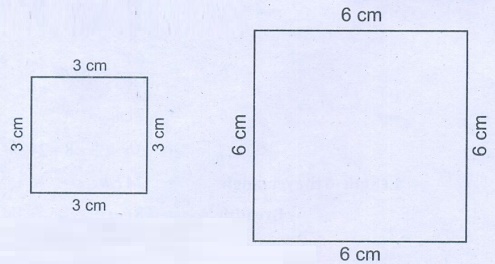
Perimeter of square A = 4 × 3 = 12 cm 

Perimeter of square B = 4 × 6 = 24 cm 

= (2 × 12) cm

2 × perimeter of square A

Perimeter of square B = Twice the Perimeter of square A.

11. What will be the area of a new square formed if the side of a square is made one-fourth?

The side of a square S = 16 cm

Area A = S × S = 16 × 16 = 256 sq.cm

The side of a new square S = one fourth of the side of original square

= 1/4 × 16 = 4

Area of the new square = 3 × S = 4 × 4 = 16 sq.cm

Area of the original square = 256 sq.cm

Area of the new square = 16 sq.cm = 256 × 1/16

= Reduced to 1 / 16 times to that of area of original square.

Area of the new square is reduced to 1/16 times to that of original area. 

12. Two plots have the same perimeter. One is a square of side 10 m and another is a rectangle of breadth 8 m. Which plot has the greater area and by how much?

Side of a square S = 10 m

Perimeter P = 4 S = 4 × 10 = 40 m

Breadth of rectangle b = 8 m  

Perimeter of rectangle = Perimeter of square

2 (l + b) = 40 m

2 (l + 8) = 40

l + 8 = 20

l = 20 – 8 = 12 m

Length l = 12 m

Area of rectangle A = l × b = 12 × 8 = 96 sq.m.

Area of square A = s × s = 10 × 10 = 100 sq.m.

Area of the square shaped plot has the greater area = (100 − 96) sq.m = 4 sq.m

Area of the square plot has the greater area than the area of the rectangular plot by 4 sq.m. 

13. Look at the picture of the house given and find the total area of the shaded portion.

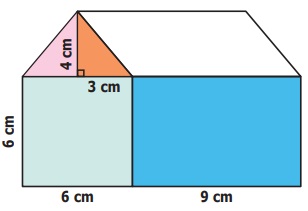
Length of the rectangle l = 9 cm

Breadth b = 6 cm

Area A  = 1 × b = 9 × 6 = 54 sq.cm

Side of the square S = 6 cm

Area A = S × S = 6 × 6 = 36 sq.cm

Area of the triangle A = 1 / 2 bh sq. units

= 1/2 × 6 × 4 sq.cm = 12 sq.cm

The total area of the shaded portion = Area of the rectangle + Area of the square + Area of the triangle

= (54 + 36 + 12) sq.cm

= 102 sq.cm

The total area of the shaded portion = 102 sq.cm

14. Find the approximate area of the flower in the given square grid.

The approximate area of the flower in the given square grid = 15.5 sq.units.

ANSWERS:

Exercise 3.2

1. i) 9 cm ii) 12 cm   2. 114 cm

3. Rahim, 120 m

4. 57 m, 2451 m²

5. ₹400/-

6. 60 cm

7. 8

8.  8 cm, 24 cm 

9. 12, (1,23), (2,22), (3,21), (4,20), (5,19), (6,18),

 (7,17), (8,16), (9,15), (10,14), (11,13), (12,12)

10. Perimeter of square B is twice that of square A

11. Area of the new square is reduced to 1/16 times to that of original area

12. Square plot by 4 m²

13. 102 cm²

14. 15.5 sq.units