Password Management

PASSWORD MANAGEMENT

Password Protection

The front line of defense against intruders is the password system. Virtually all multiuser systems require that a user provide not only a name or identifier (ID) but also a password. The password serves to authenticate the ID of the individual log- ging on to the system. In turn, the ID provides security in the following ways:

The ID determines whether the user is authorized to gain access to a system. In some systems, only those who already have an ID filed on the system are allowed to gain access.

•                           The ID determines the privileges accorded to the user. A few users may have supervisory or “superuser” status that enables them to read files and perform functions that are especially protected by the operating system. Some systems have guest or anonymous accounts, and users of these accounts have more limited privileges than others.

•                           The ID is used in what is referred to as discretionary access control. For exam- ple, by listing the IDs of the other users, a user may grant permission to them to read files owned by that user.

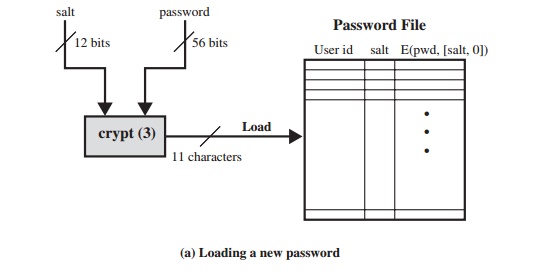
THE VULNERABILITY OF PASSWORDS To understand the nature of the threat to password-based systems, let us consider a scheme that is widely used on UNIX, in which passwords are never stored in the clear. Rather, the following procedure is employed (Figure 20.4a). Each user selects a password of up to eight printable characters in length. This is converted into a 56-bit value (using 7-bit ASCII) that serves as the key input to an encryption routine. The encryption routine, known as crypt(3), is based on DES. The DES algorithm is modified using a 12-bit “salt” value. Typically, this value is related to the time at which the password is assigned to the user. The modified DES algorithm is exercised with a data input consisting of a 64-bit block of zeros. The output of the algorithm then serves as input for a second encryption. This process is repeated for a total of 25 encryptions. The resulting 64-bit output is then translated into an 11-character sequence. The hashed password is then stored, together with a plaintext copy of the salt, in the password file for the corresponding user ID. This method has been shown to be secure against a variety of cryptanalytic attacks [WAGN00].

The salt serves three purposes:

•                           It prevents duplicate passwords from being visible in the password file. Even if two users choose the same password, those passwords will be assigned at dif- ferent times. Hence, the “extended” passwords of the two users will differ.

•                           It effectively increases the length of the password without requiring the user to remember two additional characters. Hence, the number of possible pass- words is increased by a factor of 4096, increasing the difficulty of guessing a password.

•                           It prevents the use of a hardware implementation of DES, which would ease the difficulty of a brute-force guessing attack.

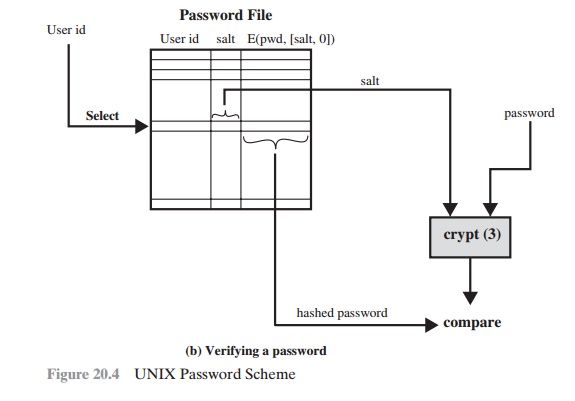
When a user attempts to log on to a UNIX system, the user provides an ID and a password. The operating system uses the ID to index into the password file and retrieve the plaintext salt and the encrypted password. The salt and user-supplied password are used as input to the encryption routine. If the result matches the stored value, the password is accepted.

The encryption routine is designed to discourage guessing attacks. Software implementations of DES are slow compared to hardware versions, and the use of 25 iterations multiplies the time required by 25. However, since the original design of this algorithm, two changes have occurred. First, newer implementations of the algorithm itself have resulted in speedups. For example, the Morris worm described in Chapter 21 was able to do online password guessing of a few hundred passwords

in a reasonably short time by using a more efficient encryption algorithm than the standard one stored on the UNIX systems that it attacked. Second, hardware per- formance continues to increase, so that any software algorithm executes more quickly.

Thus, there are two threats to the UNIX password scheme. First, a user can gain access on a machine using a guest account or by some other means and then run a password guessing program, called a password cracker, on that machine. The attacker should be able to check hundreds and perhaps thousands of possible pass- words with little resource consumption. In addition, if an opponent is able to obtain a copy of the password file, then a cracker program can be run on another machine at leisure. This enables the opponent to run through many thousands of possible passwords in a reasonable period.

As an example, a password cracker was reported on the Internet in August 1993 [MADS93]. Using a Thinking Machines Corporation parallel computer, a performance of 1560 encryptions per second per vector unit was achieved. With four vector units per processing node (a standard configuration), this works out to 800,000 encryptions per second on a 128-node machine (which is a modest size) and

            million encryptions per second on a 1024-node machine.

Even these stupendous guessing rates do not yet make it feasible for an attacker to use a dumb brute-force technique of trying all possible combinations of characters to discover a password. Instead, password crackers rely on the fact that some people choose easily guessable passwords.

Some users, when permitted to choose their own password, pick one that is absurdly short. The results of one study at Purdue University are shown in Table 20.4. The study observed password change choices on 54 machines, representing approxi- mately 7000 user accounts. Almost 3% of the passwords were three characters or fewer in length. An attacker could begin the attack by exhaustively testing all possi- ble passwords of length 3 or fewer. A simple remedy is for the system to reject any password choice of fewer than, say, six characters or even to require that all pass- words be exactly eight characters in length. Most users would not complain about such a restriction.

Password length is only part of the problem. Many people, when permitted to choose their own password, pick a password that is guessable, such as their own name, their street name, a common dictionary word, and so forth. This makes the job of password cracking straightforward. The cracker simply has to test the password file against lists of likely passwords. Because many people use guessable passwords, such a strategy should succeed on virtually all systems.

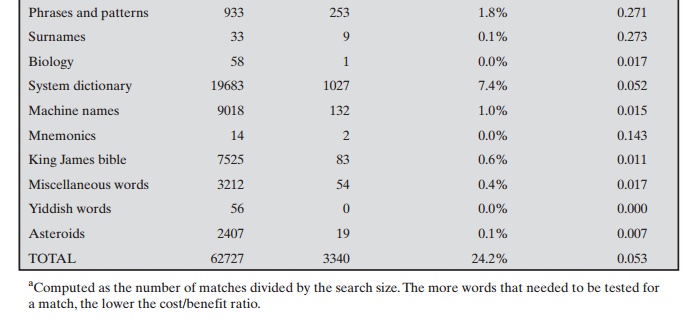
One demonstration of the effectiveness of guessing is reported in [KLEI90]. From a variety of sources, the author collected UNIX password files, containing nearly 14,000 encrypted passwords. The result, which the author rightly characterizes

Table 20.4     Observed Password Lengths [SPAF92a]

as frightening, is shown in Table 20.5. In all, nearly one-fourth of the passwords were guessed. The following strategy was used:

1.                                       Try the user’s name, initials, account name, and other relevant personal infor- mation. In all, 130 different permutations for each user were tried.

2.                                       Try words from various dictionaries. The author compiled a dictionary of over 60,000 words, including the online dictionary on the system itself, and various other lists as shown.

Table 20.5    Passwords Cracked from a Sample Set of 13,797 Accounts [KLEI90]

3.                                       Try various permutations on the words from step 2. This included making the first letter uppercase or a control character, making the entire word uppercase, reversing the word, changing the letter “o” to the digit “zero,” and so on. These permutations added another 1 million words to the list.

4.                                       Try various capitalization permutations on the words from step 2 that were not considered in step 3. This added almost 2 million additional words to the list.

Thus, the test involved in the neighborhood of 3 million words. Using the fastest Thinking Machines implementation listed earlier, the time to encrypt all these words for all possible salt values is under an hour. Keep in mind that such a thor- ough search could produce a success rate of about 25%, whereas even a single hit may be enough to gain a wide range of privileges on a system.

ACCESS CONTROL One way to thwart a password attack is to deny the opponent access to the password file. If the encrypted password portion of the file is accessible only by a privileged user, then the opponent cannot read it without already knowing the password of a privileged user. [SPAF92a] points out several flaws in this strategy:

•                           Many systems, including most UNIX systems, are susceptible to unanticipated break-ins. Once an attacker has gained access by some means, he or she may wish to obtain a collection of passwords in order to use different accounts for different logon sessions to decrease the risk of detection. Or a user with an account may desire another user’s account to access privileged data or to sabotage the system.

•                           An accident of protection might render the password file readable, thus com- promising all the accounts.

•                           Some of the users have accounts on other machines in other protection domains, and they use the same password. Thus, if the passwords could be read by anyone on one machine, a machine in another location might be compromised.

Thus, a more effective strategy would be to force users to select passwords that are difficult to guess.

Password Selection Strategies

The lesson from the two experiments just described (Tables 20.4 and 20.5) is that, left to their own devices, many users choose a password that is too short or too easy to guess. At the other extreme, if users are assigned passwords consisting of eight randomly selected printable characters, password cracking is effectively impossible. But it would be almost as impossible for most users to remember their passwords. Fortunately, even if we limit the password universe to strings of characters that are reasonably memorable, the size of the universe is still too large to permit practical cracking. Our goal, then, is to eliminate guessable passwords while allowing the user to select a password that is memorable. Four basic techniques are in use:

•                           User education

•                           Computer-generated passwords

•                 Reactive password checking

•                 Proactive password checking

Users can be told the importance of using hard-to-guess passwords and can be provided with guidelines for selecting strong passwords. This user education strat- egy is unlikely to succeed at most installations, particularly where there is a large user population or a lot of turnover. Many users will simply ignore the guidelines. Others may not be good judges of what is a strong password. For example, many users (mistakenly) believe that reversing a word or capitalizing the last letter makes a password unguessable.

Computer-generated passwords also have problems. If the passwords are quite random in nature, users will not be able to remember them. Even if the password is pronounceable, the user may have difficulty remembering it and so be tempted to write it down. In general, computer-generated password schemes have a history of poor acceptance by users. FIPS PUB 181 defines one of the best-designed auto- mated password generators. The standard includes not only a description of the approach but also a complete listing of the C source code of the algorithm. The algo- rithm generates words by forming pronounceable syllables and concatenating them to form a word. A random number generator produces a random stream of charac- ters used to construct the syllables and words.

A reactive password checking strategy is one in which the system periodically runs its own password cracker to find guessable passwords. The system cancels any passwords that are guessed and notifies the user. This tactic has a number of draw- backs. First, it is resource intensive if the job is done right. Because a determined opponent who is able to steal a password file can devote full CPU time to the task for hours or even days, an effective reactive password checker is at a distinct disad- vantage. Furthermore, any existing passwords remain vulnerable until the reactive password checker finds them.

The most promising approach to improved password security is a proactive password checker. In this scheme, a user is allowed to select his or her own pass- word. However, at the time of selection, the system checks to see if the password is allowable and, if not, rejects it. Such checkers are based on the philosophy that, with sufficient guidance from the system, users can select memorable passwords from a fairly large password space that are not likely to be guessed in a dictionary attack.

The trick with a proactive password checker is to strike a balance between user acceptability and strength. If the system rejects too many passwords, users will complain that it is too hard to select a password. If the system uses some simple algorithm to define what is acceptable, this provides guidance to password crackers to refine their guessing technique. In the remainder of this subsection, we look at possible approaches to proactive password checking.

The first approach is a simple system for rule enforcement. For example, the following rules could be enforced:

•                 All passwords must be at least eight characters long.

•                 In the first eight characters, the passwords must include at least one each of uppercase, lowercase, numeric digits, and punctuation marks.

These rules could be coupled with advice to the user. Although this approach is superior to simply educating users, it may not be sufficient to thwart password crackers. This scheme alerts crackers as to which passwords not to try but may still make it possible to do password cracking.

Another possible procedure is simply to compile a large dictionary of possible “bad” passwords. When a user selects a password, the system checks to make sure that it is not on the disapproved list. There are two problems with this approach:

•                           Space: The dictionary must be very large to be effective. For example, the dic- tionary used in the Purdue study [SPAF92a] occupies more than 30 megabytes of storage.

•                           Time: The time required to search a large dictionary may itself be large. In addition, to check for likely permutations of dictionary words, either those words most be included in the dictionary, making it truly huge, or each search must also involve considerable processing.

Two techniques for developing an effective and efficient proactive password checker that is based on rejecting words on a list show promise. One of these develops a Markov model for the generation of guessable passwords [DAVI93]. Figure 20.5 shows a simplified version of such a model. This model shows a language consisting of an alphabet of three characters. The state of the system at any time is the identity of the most recent letter. The value on the transition from one state to another repre- sents the probability that one letter follows another. Thus, the probability that the next letter is b, given that the current letter is a, is 0.5.

In general, a Markov model is a quadruple [m, A, T, k], where m is the number of states in the model, A is the state space, T is the matrix of transition probabilities, and k is the order of the model. For a kth-order model, the probability of making a transition to a particular letter depends on the previous k letters that have been gen- erated. Figure 20.5 shows a simple first-order model.

The authors report on the development and use of a second-order model. To begin, a dictionary of guessable passwords is constructed. Then the transition matrix is calculated as follows:

1.                        Determine the frequency matrix f, where f(i, j, k) is the number of occurrences of the trigram consisting of the ith, jth, and kth character. For example, the password parsnips yields the trigrams par, ars, rsn, sni, nip, and ips.

2.                        For each bigram ij, calculate f(i, j, inf) as the total number of trigrams beginning with ij. For example, f(a, b, inf) would be the total number of trigrams of the form aba, abb, abc, and so on.

3.                        Compute the entries of T as follows:

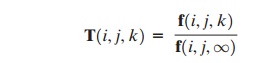
The result is a model that reflects the structure of the words in the dictionary. With this model, the question “Is this a bad password?” is transformed into the question “Was this string (password) generated by this Markov model?” For a given password, the transition probabilities of all its trigrams can be looked up. Some stan- dard statistical tests can then be used to determine if the password is likely or unlikely for that model. Passwords that are likely to be generated by the model are rejected. The authors report good results for a second-order model. Their system catches virtually all the passwords in their dictionary and does not exclude so many potentially good passwords as to be user unfriendly.

A quite different approach has been reported by Spafford [SPAF92a, SPAF92b]. It is based on the use of a Bloom filter [BLOO70]. To begin, we explain the operation of the Bloom filter. A Bloom filter of order k consists of a set of k independent hash functions H1(x), H2(x),…….., Hk(x), where each function maps a password into a hash value in the range 0 to N - 1. That is,

1.                        A hash table of N bits is defined, with all bits initially set to 0.

2.                        For each password, its k hash values are calculated, and the corresponding bits in the hash table are set to 1. Thus, if Hi(Xj) = 67 for some (i, j), then the sixty- seventh bit of the hash table is set to 1; if the bit already has the value 1, it remains at 1.

When a new password is presented to the checker, its k hash values are calcu- lated. If all the corresponding bits of the hash table are equal to 1, then the password is rejected. All passwords in the dictionary will be rejected. But there will also be some “false positives” (that is, passwords that are not in the dictionary but that pro- duce a match in the hash table). To see this, consider a scheme with two hash func- tions. Suppose that the passwords undertaker and hulkhogan are in the dictionary, but xG%#jj98 is not. Further suppose that

If the password xG%#jj98 is presented to the system, it will be rejected even though it is not in the dictionary. If there are too many such false positives, it will be difficult for users to select passwords. Therefore, we would like to design the hash scheme to minimize false positives. It can be shown that the probability of a false positive can be approximated by:

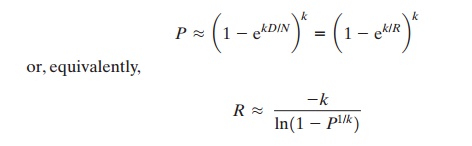
where

k = number of hash functions

N = number of bits in hash table

D = number of words in dictionary

R = N/D, ratio of hash table size (bits) to dictionary size (words)

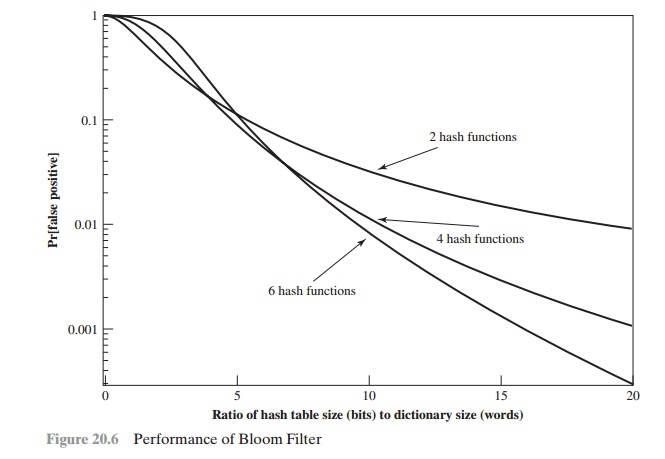
Figure 20.6 plots P as a function of R for various values of k. Suppose we have a dictionary of 1 million words and we wish to have a 0.01 probability of rejecting a password not in the dictionary. If we choose six hash functions, the required ratio is R = 9.6. Therefore, we need a hash table of 9.6 * 106 bits or about 1.2 MBytes of storage. In contrast, storage of the entire dictionary would require on the order of 8 MBytes. Thus, we achieve a compression of almost a factor of 7. Furthermore, password checking involves the straightforward calculation of six hash functions and is independent of the size of the dictionary, whereas with the use of the full dictionary, there is substantial searching.