Operations Research Models

OPERATIONS RESEARCH MODELS

Imagine that you have a 5-week business commitment between Fayetteville (FYV) and Denver (DEN). You fly out of Fayetteville on Mondays and return on Wednesdays. A regular round-trip ticket costs $400, but a 20% discount is granted if the dates of the ticket span a weekend. A one-way ticket in either direction costs 75% of the reg-ular price. How should you buy the tickets for the 5-week period?

We can look at the situation as a decision-making problem whose solution re-quires answering three questions:

1. What are the decision alternatives?

2. Under what restrictions is the decision made?

3. What is an appropriate objective criterion for evaluating the alternati-ves?

Three alternatives are considered:

Buy five regular FYV-DEN-FYV for departure on Monday and return on Wednes-day of the same week.

Buy one FYV-DEN, four DEN-FYV-DEN that span weekends, and one DEN-FYV.

Buy one FYV-DEN-FYV to cover Monday of the first week and Wednesday of  the last week and four DEN-FYV-DEN to cover the remaining legs. All tickets in this alternative span at least one weekend.

The restriction on these options is that you should be able to leave FYV on Monday and return on Wednesday of the same week.

An obvious objective criterion for evaluating the proposed alternative is the price of the tickets. The alternative that yields the smallest cost is the best. Specifically, we have

Alternative 1 cost = 5 X  400 = $2000

Alternative 2 cost = .75  X  400 + 4 X  (.8 X  400)  + .75  X  400 = $1880

Alternative 3 cost =  5 X  (.8 X  400)  =  $1600

Thus, you should choose alternative 3.

Though the preceding example illustrates the three main components of an OR model-alternatives, objective criterion, and constraints-situations differ in the de-tails of how each component is developed and constructed. To illustrate this point, con-sider forming a maximum-area rectangle out of a piece of wire of length L inches. What should be the width and height of the rectangle?

In contrast with the tickets example, the number of alternatives in the present ex-ample is not finite; namely, the width and height of the rectangle can assume an infinite number of values. To formalize this observation, the alternatives of the problem are identified by defining the width and height as continuous (algebraic) variables.

Let

w = width of the rectangle in inches

h = height of the rectangle in inches

Based on these definitions, the restrictions of the situation can be expressed verbally as

Width of rectangle + Height of rectangle =  Half the length of the wire

Width and height cannot be negative

These restrictions are translated algebraically as

2(w + h)  = L

w  >= 0, h >=  0

The only remaining component now is the objective of the problem; namely, maximization of the area of the rectangle. Let z be the area of the rectangle, then the complete model becomes

Maximize z = wh

subject to

2(w + h)  = L

w, h 2 >= 0

The optimal solution of this model is w = h = L/4, which calls for constructing a square shape.

Based on the preceding two examples, the general OR model can be organized in the following general format:

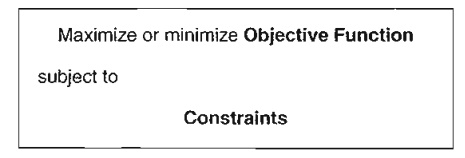
A solution of the mode is feasible if it satisfies all the constraints. It is optimal if, in addition to being feasible, it yields the best (maximum or minimum) value of the objective function. In the tickets example, the problem presents three feasible alternatives, with the third alternative yielding the optimal solution. In the rectangle problem, a feasible alternative must satisfy the condition w + h = L/2 with wand h assuming nonnegative values. This leads to an infinite number of feasible solutions and, unlike the tickets problem, the optimum solution is determined by an appropriate mathematical tool (in this case, differential calculus).

Though OR models are designed to "optimize" a specific objective criterion subject to a set of constraints, the quality of the resulting solution depends on the completeness of the model in representing the real system. Take, for example, the tickets model. If one is not able to identify all the dominant alternatives for purchasing the tick-ets, then the resulting solution is optimum only relative to the choices represented in the model. To be specific, if alternative 3 is left out of the model, then the resulting "optimum" solution would call for purchasing the tickets for $1880, which is a suboptimal solution. The conclusion is that "the" optimum solution of a model is best only for that model. If the model happens to represent the real system reasonably well, then its solution is optimum also for the real situation.

PROBLEM SET 1.1A

1. In the tickets example, identify a fourth feasible alternative.

2. In the rectangle problem, identify two feasible solutions and determine which one is better.

3. Determine the optimal solution of the rectangle problem. (Hint: Use the constraint to express the objective function in terms of one variable, then use differential calculus.)