Newton Raphson Method -Unconstrained Problems

The Newton-Raphson Method

In general, the necessary condition equations, Ñ f(X) = 0, may be difficult to solve numerically. The Newton-Raphson method is an iterative procedure for solving simultaneous nonlinear equations.

Consider the simultaneous equations

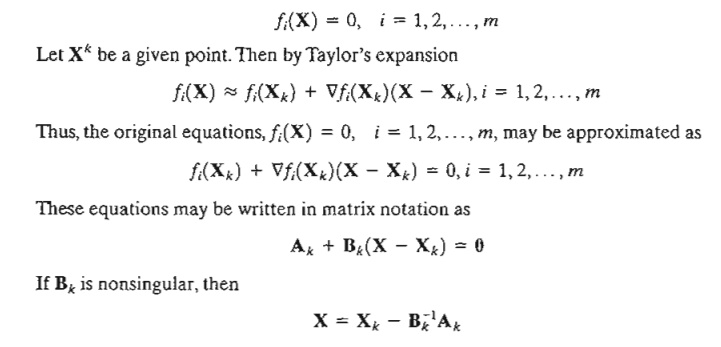
The idea of the method is to start from an initial point X o and then use the equation above to determine a new point. The process continues until two successive points, X k and X k +1 are approximately equal.

A geometric interpretation of the method is illustrated by a single-variable function in Figure 18.3. The relationship between xk and xk+1 for a single-variable function f(x) reduces to

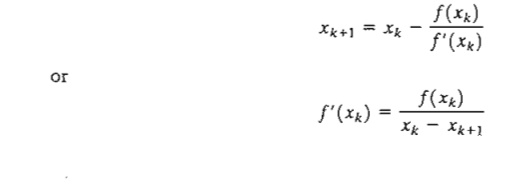
FIGURE 18.3

Illustration of the iterative process in the Newton-Raphson method

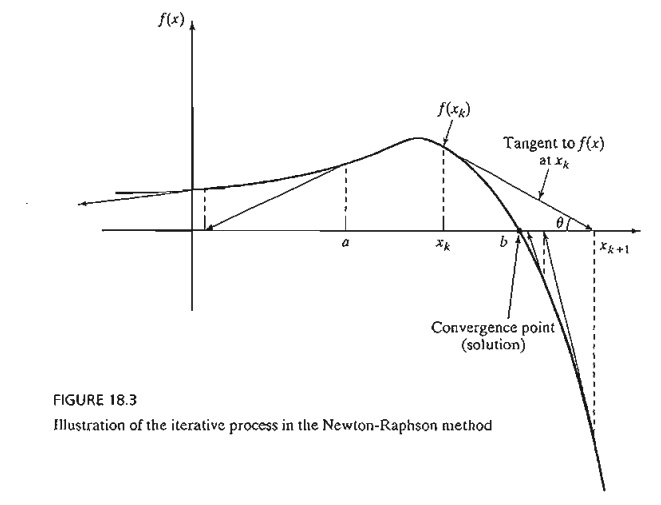
The figure shows that xk+1 is determined from the slope of f(x) at xk where tan q = f' (xk).

One difficulty with the method is that convergence is not always guaranteed unless the function f is well behaved. In Figure 18.3, if the initial point is a, the method will diverge. In general, trial and error is used to locate a "good" initial point.

Example 18.1-3

To demonstrate the use of the Newton-Raphson method, consider determining the stationary points of the function

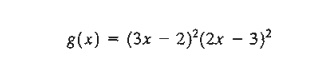
To determine the stationary points, we need to solve

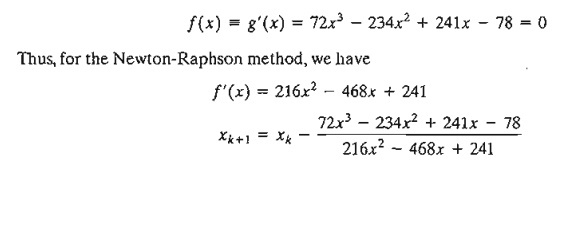
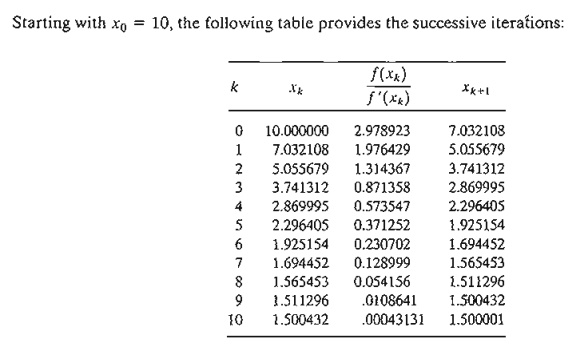
The method converges to x = 1.5. Actually, f(x) has three stationary points at x = 2/3, x = 13/12, and x = 3/2. The remaining two points can be found by selecting different values for initial xo. In fact, xo = .5 and xo = 1 should yield the missing stationary points.

Excel Moment

Template excelNR.xls can be used to solve any single-variable equation. It requires entering f(x)/f' (x) in cell C3. For Example 18.1-3, we enter

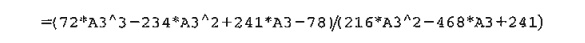
The variable x is replaced with A3. The template allows setting a tolerance limit Δ, which specifies the allowable difference between xk and xk+1 that signals the termination of the iterations. You are encouraged to use different initial xo to get a feel of how the method works.

In general, the Newton-Raphson method requires making several attempts before "all" the solutions can be found. In Example 18.1-3, we know beforehand that the equa-tion has three roots. This will not be the case with complex or multi-variable functions, however.

PROBLEM SET 18.1B

1.     Use NewtonRaphson.xls to solve Problem I(c), Set I8.la.

2.     Solve Problem 2(b), Set I8.la by the Newton-Raphson method.