NP Hard and NP Completeness

INTRODUCTION TO NP-HARD AND NP-COMPLETENESS

P: the class of decision problems that are solvable in O(p(n)) time, where p(n) is a polynomial of problem‘s input size n

Examples:

b  searching

b element uniqueness b graph connectivity b graph acyclicity

primality testing (finally proved in 2002)

NP (nondeterministic polynomial): class of decision problems whose proposed solutions can be verified in polynomial time = solvable by a nondeterministic polynomial algorithm

A nondeterministic polynomial algorithm is an abstract two-stage procedure that: b generates a random string purported to solve the problem

b  checks whether this solution is correct in polynomial time

E.g. Problem: Is a boolean expression in its conjunctive normal form (CNF) satisfiable, i.e., are there values of its variables that makes it true?

This problem is in NP. Nondeterministic algorithm: b Guess truth assignment

b Substitute the values into the CNF formula to see if it evaluates to true Example: (A | ¬B | ¬C) & (A | B) & (¬B | ¬D | E) & (¬D | ¬E)

Truth assignments:

A B C D E 0 0 0 0 0

.  .  .

1 1 1 1 1

Checking phase: O(n)

1. PROBLEMS ARE IN NP?

b  Hamiltonian circuit existence

b       Partition problem: Is it possible to partition a set of n integers into two disjoint subsets with the same sum?

b       Decision versions of TSP, knapsack problem, graph coloring, and many other combinatorial optimization problems. (Few exceptions include: MST, shortest paths)

b       All the problems in P can also be solved in this manner (but no guessing is necessary), so we have:

 P inculde NP

b  Big question:  P = NP ?

NP problems

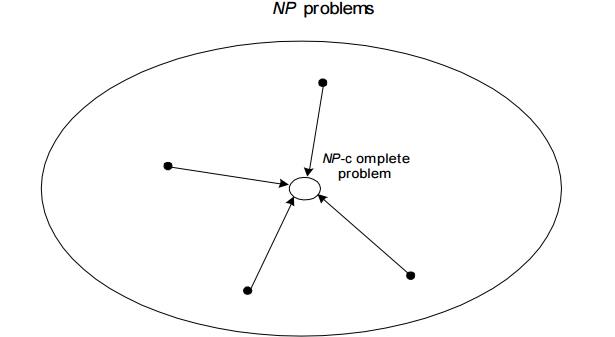
NP Hard problem:

–   Most problems discussed are efficient (poly time)

–   An interesting set of hard problems: NP-complete.

•         A decision problem D is NP-complete if it‘s as hard as any problem in NP, i.e.,  D is in NP

  every problem in NP is polynomial-time reducible to D

Cook’s theorem (1971): CNF-sat is NP-complete

Other NP-complete problems obtained through polynomial-time reductions from a known NP-complete problem

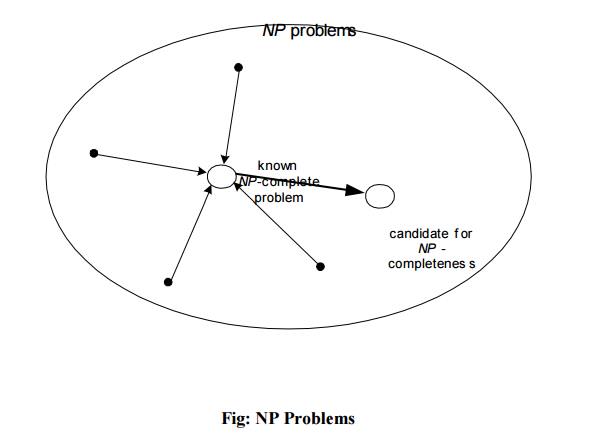
Fig: NP Problems

Examples:

TSP, knapsack, partition, graph-coloring and hundreds of other problems of combinatorial nature

v   P = NP would imply that every problem in NP, including all NP-complete problems, could be solved in polynomial time

v   If a polynomial-time algorithm for just one NP-complete problem is discovered,

then every problem in NP can be solved in polynomial time, i.e., P = NP

v        Most but not all researchers believe that P NP , i.e. P is a proper subset of NP