Connected Component and Biconnected Components

CONNECTED COMPONENT

A connected component of a graph G is a maximal connected induced subgraph, that is, a connected induced subgraph that is not itself a proper subgraph of any other connected subgraph of G

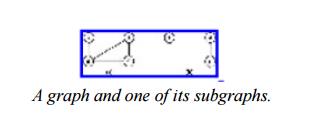
A graph and one of its subgraphs.

The above Figure is a connected graph. It has only one connected component, namely itself. Following figure is a graph with two connected components.

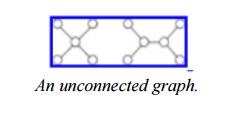
1. BICONNECTED COMPONENTS

An articulation point of a graph is a vertex v such that when we remove v and all edges incident upon v , we break a connected component of the graph into two or more pieces.

A connected graph with no articulation points is said to be biconnected. Depth-first search is particularly useful in finding the biconnected components of a graph.

The problem of finding articulation points is the simplest of many important problems concerning the connectivity of graphs. As an example of applications of connectivity algorithms, we may represent a communication network as a graph in which the vertices are sites to be kept in communication with one another.

A graph has connectivity k if the deletion of any k-1 vertices fails to disconnect the graph. For example, a graph has connectivity two or more if and only if it has no articulation points, that is, if and only if it is biconnected.

The higher the connectivity of a graph, the more likely the graph is to survive the failure of some of its vertices, whether by failure of the processing units at the vertices or external attack.

We shall here give a simple depth-first search algorithm to find all the articulation points of a connected graph, and thereby test by their absence whether the graph is biconnected.

1. Perform a depth-first search of the graph, computing dfnumber [v] for each vertex v. In essence, dfnumber orders the vertices as in a preorder traversal of the depth-first spanning tree.

2. For each vertex v, compute low [v], which is the smallest dfnumber of v or of any vertex w reachable from v by following down zero or more tree edges to a descendant x of v (x may be v) and then following a back edge (x, w). We compute low [v] for all vertices v by visiting the vertices in a postorder traversal. When we process v, we have computed low [y] for every child y of v. We take low [v] to be the minimum of a. dfnumber [v],b. dfnumber [z] for any vertex z for which there is a back edge (v, z) and c. low [y] for any child y of v.

Now we find the articulation points as follows.

a.    The root is an articulation point if and only if it has two or more children. Since there are no cross edges, deletion of the root must disconnect the subtrees rooted at its children, as a disconnects {b, d, e} from {c, f, g} in Fig..

b.   A vertex v other than the root is an articulation point if and only if there is some child w of v such that low [w] ≥ dfnumber [v]. In this case, v disconnects w and its descendants from the rest of the graph. Conversely, if low [w] < dfnumber [v], then there must be a way to get from w down the tree and back to a proper ancestor of v (the vertex whose dfnumber is low [w]), and therefore deletion of v does not disconnect w or its descendants from the rest of the graph.