Depth First Search(DFS) Algorithm: Working Principle, Forest, Application

DEPTH FIRST SEARCH

WORKING PRINCIPLE

♦ Depth-first search starts visiting vertices of a graph at an arbitrary vertex by marking it as having been visited.

♦ On each iteration, the algorithm proceeds to an unvisited vertex that is adjacent to the one it is currently in.

♦ The algorithm stops, when there is no unvisited adjacent unvisited vertex.

♦ At a dead end, the algorithm backs up one edge to the vertex it came from and tries to continue visiting unvisited vertices from there.

♦ The algorithm eventually halts, when there is no unvisited unvisited vertex.

♦ Stack is used totrace the operation of depth-first search.

♦     Push a vertex onto the stack when the vertex is reached for the first time (i.e., the visit of the vertex starts), and pop a vertex off the stack when it becomes a dead end (i.e., the visit of the vertex ends).

1. DEPTH FIRST SEARCH FOREST

♦ It is also very useful to accompany a depth-first search traversal by constructing the so called depth-first search forest.

♦       The traversal's starting vertex serves as the root of the first tree in such a forest. Whenever a new unvisited vertex is reached for the first time, it is attached as a child to the vertex from which it is being reached. Such an edge is called a tree edge because the set of all such edges forms a forest.

♦  The algorithm may also encounter an edge leading to a previously visited vertex other than its immediate predecessor (i.e., its parent in the tree). Such an edge is called a back edge because it connects a vertex to its ancestor, other than the parent, in the depth-first search forest.

♦ Here is a pseudo code of the depth-first search.

2. ALGORITHM DFS(G)

Algorithm Dfs(G)

//Implements a depth-first search traversal of a given graph //Input: Graph G = (V, E)

//0utput: Graph G with its vertices marked with consecutive integers in the order they've been first encountered by the DFS traversal mark each vertex in V with 0 as a mark of being "unvisited"

count ^! 0

for each vertex v in V do

if v is marked with 0 dfs (v)

dfs(v)

//visits recursively all the unvisited vertices connected to vertex v and assigns them the numbers in the order they are encountered via global variable count count ^!count + 1; mark v with count

for each vertex w in V adjacent to v do if w is marked with 0

dfs(w)

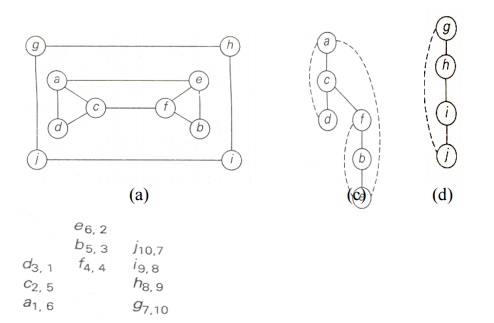
Fig: Example of a DFS traversal

(a) Graph. (b) Traversal's stack (the first subscript number indicates the order in which a vertex was visited, i.e., pushed onto the stack; the second one indicates the order in which it became a dead-end, i.e., popped off the stack). (c) DFS forest (with the tree edges shown with solid lines and the back edges shown with dashed lines).

♦   A DFS traversal itself and the forest-like representation of a graph it provides have proved to be extremely helpful for the development of efficient algorithms for checking many important properties of graphs.

♦ DFS yields two orderings of vertices:

1. The order in which the vertices are reached for the first time (pushed onto the stack)

2. The order in which the vertices become dead ends (popped off the stack).

These orders are qualitatively different, and various applications can take advantage of either of them.

3. APPLICATIONS OF DFS

♦ DFS is used for

♦ Checking connectivity of the graph

♦ Checking a cyclicity of a graph.

Checking connectivity of the graph

♦   Checking a graph's connectivity can be done as follows.

♦ Start a DFS traversal at an arbitrary vertex

♦ Check, after the algorithm halts, whether all the graph's vertices will have been visited.

♦ If they have, the graph is connected; otherwise, it is not connected

Checking a cyclicity of a graph

♦ If there is a back edge  in DFS forest , then the graph is acyclic.

♦  If there is a back edge,from some vertex u to its ancestor v (e.g., the back edge from d to a in Figure 5.5c), the graph has a cycle that comprises the path from :J to u via a sequence of tree edges in the DFS forest followed by the back edge from u to v.

Articulation point

♦ A vertex of a connected graph is said to be its articulation point if its removal with all edges incident to it breaks the graph into disjoint pieces.