Model of Uncontrolled two Area Load Frequency Control System

MODEL OF UNCONTROLLED TWO AREA LOAD FREQUENCY CONTROL SYSTEM

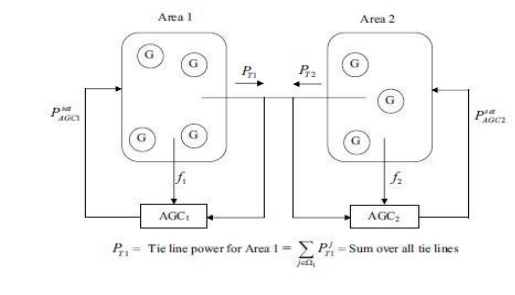
AGC IN A MULTI AREA SYSTEM

Ø     In an interconnected (multi area) system, there will be one ALFC loop for each control area (located at the ECC of that area).

 They are combined as shown in Fig for the interconnected system operation.

 For a total change in load of ∆PD, the steady state Consider a two area system as depicted in Figure.

 The two secondary frequency controllers, AGC1 and AGC2, will adjust the power reference values of the generators participating in the AGC.

 In an N-area system, there are N controllers AGCi, one for each area i.

A block diagram of such a controller is given in Figure 4.2. A common way is to implement this as a proportional-integral (PI) controller:

Deviation in frequency in the two areas is given by

∆f=∆ω1=∆ω2=−∆PD / β1 + β2

where

β1 = D1 + 1/ R1

β2= D2+1/R2

E expression for tie-line flow in a two-area interconnected system Consider a change in load

∆PD1 in area1. The steady state frequency deviation ∆f is the same for both the areas.

That is ∆f =∆f1 =∆f2.

Thus, for area1, we have ∆Pm1 -∆PD1 -∆P12 = D1∆f

Where, Area 2 ∆P12 is the tie line power flow from Area1to Area 2; and for ∆Pm2 +∆P12 = D2∆f

The mechanical power depends on regulation.

Hence ∆Pm1= -∆f 1∆Pm2= -∆f 2 Substituting these equations, yields (1/R1+ D1) ∆f =-∆P12- ∆Pm

(1/R2+ D2) ∆f =-∆P12- ∆Pm

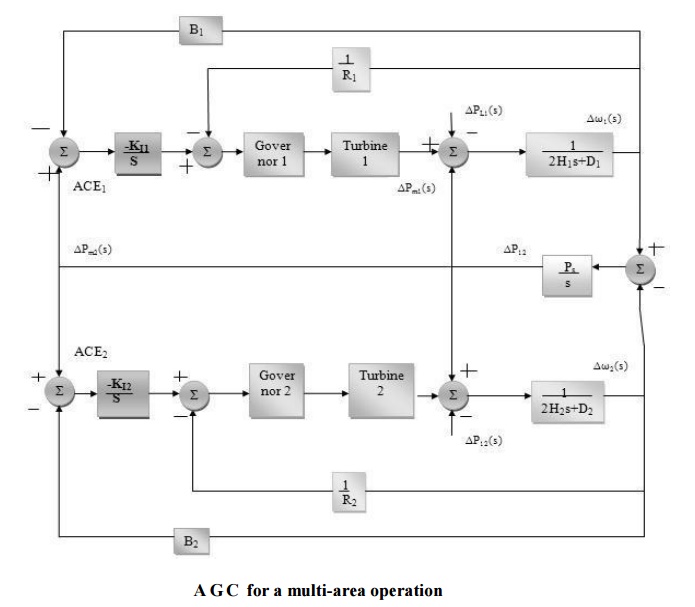
Solving for ∆f, we get

∆f= -∆PD1/ β1 + β2

Where β1 and β2  are the composite frequency response characteristic of Area1 and Area 2 respectively. An increase of load in area1 by ∆PD1 results in a frequency reduction in both areas and a tie-line flow of ∆P12. A positive ∆P12 is indicative of flow from Area1 to Area

2 while a negative ∆P12 means flow from Area 2 to Area1. Similarly, for a change in Area 2 load by ∆PD2, we have

∆f= -∆PD2/ β1 + β2