Chapter: Power System Operation and Control : Real Power Frequency Control
LFC Control of Single Area and Derive the Steady State
LFC CONTROL OF SINGLE AREA AND DERIVE THE STEADY STATE
FREQUENCY ERROR
All the individual blocks can now be connected to represent the complete ALFC loop as
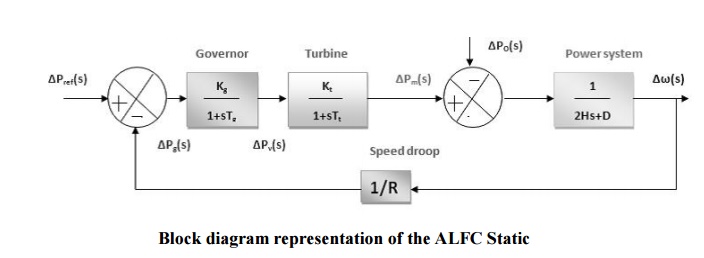
Power Generation
We have
∆PG(s) = kGkt / (1+sTG)(1+sTt)[∆Pc(s)-1/R∆F(s)]
The generator is synchronized to a network of very large size. So, the speed or frequency will be essentially independent of any changes in a power output of the generator
ie, ∆F(s) =0
Therefore ∆PG(s) =kGkt / (1+sTg) (1+sTt)* ∆Pc(s)
Steady state response
(i)Controlled case:
To find the resulting steady change in the generator output:
Let us assume that we made a step change of the magnitude ∆Pc of the speed changer For step change, ∆Pc(s) = ∆Pc/s
∆PG(s) =kGkt/ (1+sTg) (1+sTt). ∆Pc(s)/s s∆PG (s) =kGkt/ (1+sTg) (1+sTt). ∆Pc(s)
Applying final value theorem,
∆PG (stat) = ∆
(ii)Uncontrolled case
Let us assume that the load suddenly increases by small amount ∆PD.
Consider there is no external work and the generator is delivering a power to a single load.
∆Pc = 0
Kg Kt = 1
∆PG(s) = 1/ (1+sTG) (1+sTt) [-∆F(s)/R]
For a step change ∆F(s) = ∆f/s
Therefore
∆PG(s) = 1/(1+sTG)(1+sTt)[-∆F/sR]
∆f/∆PG (stat) =-R Hz/MW
Steady State Performance of the ALFC Loop
In the steady state, the ALFC is in „open‟ state, and the output is obtained by substituting s→0 in the TF.
With s→0, Gg(s) and Gt(s) become unity, then,(note that
∆Pm =∆PT = PG =∆Pe = ∆PD;
That is turbine output = generator/electrical output = load demand)
∆Pm = ∆Pref – (1/R) ∆ω or ∆Pm = ∆Pref – (1/R)∆f
When the generator is connected to infinite bus (∆f = 0, and ∆V = 0), then
∆ Pm = ∆Pref . If the network is finite, for a fixed speed changer setting (∆Pref = 0), then
∆Pm = (1/R)∆f
or
∆f=RPm.
Concept of AGC (Supplementary ALFC Loop)
Ø The ALFC loop shown in Fig. is called the primary ALFC loop.
Ø It achieves the primary goal of real power balance by adjusting the turbine output ∆Pm to match the change in load demand ∆PD.
Ø All the participating generating units contribute to the change in generation. But a change in load results in a steady state frequency deviation ∆f.
Ø The restoration of the frequency to the nominal value requires an additional control loop called the supplementary loop.
Ø This objective is met by using integral controller which makes the frequency deviation zero.
Ø The ALFC with the supplementary loop is generally called the AGC. The block diagram of an AGC is shown in Fig.
Ø The main objectives of AGC a r e
i) to regulate the frequency (using both primary and supplementary controls);
ii) and to maintain the scheduled tie-line flows.
A secondary objective of the AGC is to distribute the required change in generation among the connected generating units economically (to obtain least operating costs).

AGC in a Single Area System
In a single area system, there is no tie-line schedule to be maintained.
Thus the function of the AGC is only to bring the frequency to the nominal value.
This will be achieved using the supplementary loop (as shown in Fig.) which uses the integral controller to change the reference power setting so as to change the speed set point.
The integral controller gain KI n e e d s to be adjusted for satisfactory response (in terms of overshoot, settling time) of the system.
Although each generator will be having a separate speed governor, all the generators in the control area are replaced by a single equivalent generator, and the ALFC for the area corresponds to this equivalent generator.
Related Topics