Chapter: Mechanical : Heat and Mass Transfer : Convection
Methods for Determining Heat Transfer Coefficient
Methods for
Determining Heat Transfer Coefficient
The convective heat transfer coefficient in forced flow can be evaluated by:
(a) Dimensional Analysis combined with experiments;
(b) Reynolds Analogy –an analogy between heat and momentum transfer;
(c) Analytical Methods –exact and approximate analyses of boundary layer
equations.
Method of Dimensional Analysis
As pointed out in Chapter 5, dimensional analysis does not yield equations which can be solved. It simply combines the pertinent variables into non-dimensional numbers which facilitate the interpretation and extend the range of application of experimental data. The relevant variables for forced convection heat transfer phenomenon whether laminar or turbulent, are
(b) the properties of the fluid –density p, specific heat capacity Cp, dynamic or absolute viscosity m, thermal conductivity k.
(ii) the properties of flow –flow velocity Y, and the characteristic dimension of the system L.
As such, the convective heat transfer coefficient, h, is written as h = f ( r, V, L, m, Cp,
k) = 0 (5.14)
Since there are seven variables and four primary dimensions, we would expect three dimensionless numbers. As before, we choose four independent or core variables as r,V, L, k, and calculate the dimensionless numbers by applying Buckingham p’s method:
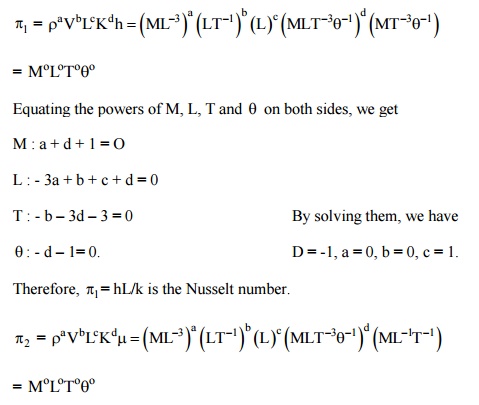
Equating the powers of M, L, T and on both sides, we get
M : a + d +1 = 0
L : - 3a + b + c + d = 1 = 0
T : - b –3d –1 = 0
q: - d = 0.
By solving them, d = 0, b = - 1, a = - 1, c = - 1
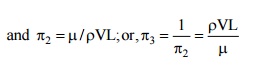
(Reynolds number is a flow parameter of greatest significance. It is the ratio of inertia forces to viscous forces and is of prime importance to ascertain the conditions under which a flow is laminar or turbulent. It also compares one flow with another provided the corresponding length and velocities are comparable in two flows. There would be a similarity in flow between two flows when the Reynolds numbers are equal and the geometrical similarities are taken into consideration.)
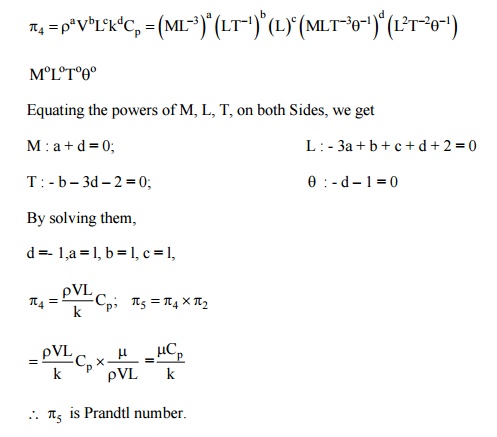
Therefore, the functional relationship is expressed as:
Nu = f (Re, Pr); or Nu = C Rem Prn (5.15)
where the values of c, m and n are determined experimentally.
Principles of Reynolds Analogy
Reynolds was the first person to observe that there exists a similarity between the exchange of momentum and the exchange of heat energy in laminar motion and for that reason it
has been termed ‘Reynolds analogy’. Let us c flowing over a plane wall. The X-coordinate is measured parallel to the surface and the V-
coordinate is measured normal to it. Since all fluids are real and viscous, there would be a thin layer, called momentum boundary layer, in the vicinity of the wall where a velocity gradient normal to the direction of flow exists. When the temperature of the surface of the wall is different than the temperature of the fluid stream, there would also be a thin layer, called thermal boundary layer, where there is a variation in temperature normal to the direction of flow. Fig. 2.6 depicts the velocity distribution and temperature profile for the laminar motion of the fluid flowing past a plane wall.
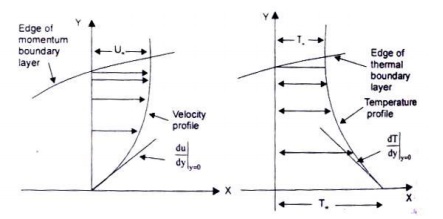
Fig. velocity distribution and temperature profile for laminar motion of the fluid over a plane surface

Equation (5.18) is satisfactory for gases in which Pr is approximately equal to unity. Colburn has shown that Eq. (5.18) can also be used for fluids having Prandtl numbers ranging from 0.6 to about 50 if it is modified in accordance with experirnental results.
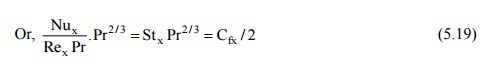
Eq. (5.19) expresses the relation between fluid friction and heat transfer for laminar flow over a plane wall. The heat transfer coefficient could thus be determined by making measurements of the frictional drag on a plate under conditions in which no heat transfer is involved.
Analytical Evaluation of ‘h’–Assumptions for Laminar
As pointed out earlier, when the motion of the fluid is caused by the imposition of external forces, such as pressure differences, and the fluid flows over a solid surface, at a temperature different from the temperature of the fluid, the mechanism of heat transfer is called
‘forced convection’. Therefore, any analytica coefficient would require the temperature distribution in the flow field surrounding the body.
That is, the theoretical analysis would require the use of the equation of motion of the viscous fluid flowing over the body along with the application of the principles of conservation of mass and energy in order to relate the heat energy that is convected away by the fluid from the solid surface.
For the sake of simplicity, we will consider the motion of the fluid in 2 space dimension, and a steady flow. Further, the fluid properties like viscosity, density, specific heat, etc are constant in the flow field, the viscous shear forces m the Y –direction is negligible and there are no variations in pressure also in the Y –direction.
Derivation of the Equation of Continuity–Conservation of Mass
We choose a control volume within the laminar boundary layer as shown in Fig. 6.2. The mass will enter the control volume from the left and bottom face and will leave the control volume from the right and top face. As such, for unit depth in the Z-direction,

For steady flow conditions, the net efflux of mass from the control volume is zero, therefore,

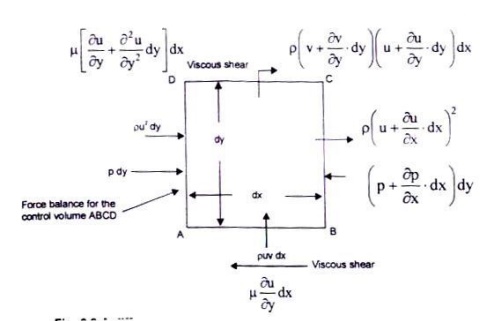
Fig. 2.7 a differential control volume within the boundary layer for laminar flow over a plane wall
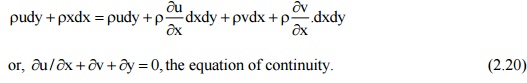
or, ¶u / x¶ +v ¶y +0,¶the =equation of continuity. (2.20)
Related Topics