Concept of Critical Thickness of Insulation

Concept of Critical Thickness of Insulation

The addition of insulation at the outside surface of small pipes may not reduce the rate of heat transfer. When an insulation is added on the outer surface of a bare pipe, its outer radius, r0 increases and this increases the thermal resistance due to conduction logarithmically whereas t he thermal resistance to heat flow due to fluid film on the outer surface decreases linearly with increasing radius, r0. Since the total thermal resistance is proportional to the sum of these two resistances, the rate of heat flow may not decrease as insulation is added to the bare pipe.

Fig. 2.7 shows a plot of heat loss against the insulation radius for two different cases. For small pipes or wires, the radius rl may be less than re and in that case, addition of insulation to the bare pipe will increase the heat loss until the critical radius is reached. Further addition of insulation will decrease the heat loss rate from this peak value. The insulation thickness (r* –rl) must be added to reduce the heat loss below the uninsulated rate. If the outer pipe radius rl is greater than the critical radius re any insulation added will decrease the heat loss.

Expression for Critical Thickness of Insulation for a Cylindrical Pipe

Let us consider a pipe, outer radius rl as shown in Fig. 2.18. An insulation is added such that the outermost radius is r a variable and the insulation thickness is (r –rI). We assume that the thermal conductivity, k, for the insulating material is very small in comparison with the thermal conductivity of the pipe material and as such the temperature T1, at the inside surface of the insulation is constant. It is further assumed that both h and k are constant. The rate of heat flow, per unit length of pipe, through the insulation is then,

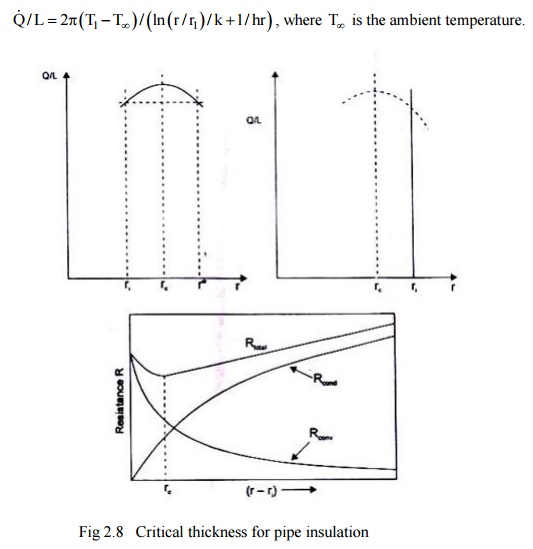
which is always a negative quantity. Thus, the optimum radius, rc = k/h will always give a maximum heal loss and not a minimum.

An Expression for the Critical Thickness of Insulation for a Spherical Shell

Let us consider a spherical shell having an outer radius r1 and the temperature at that surface T1 . Insulation is added such that the outermost radius of the shell is r, a variable. The thermal conductivity of the insulating mater

ial, k, the convective heat transfer coefficient at the outer surface, h, and the ambient temperature T ¥ is constant. The rate of heat transfer through the insulation on the spherical shell is given by

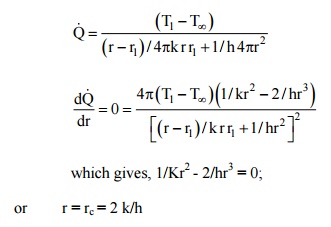
INTERNAL FLOW THROUGH TUBES :

Thermal conditionsLaminar or turbulent entrance flow and fully developed thermal condition For laminar flows the thermal entrance length is a function of the Reynolds number and the is the thermal diffusitivity.