Evaluation of Convective Heat Transfer Coefficient

Evaluation of Convective Heat Transfer Coefficient

The convective heat transfer coefficient in free or natural convection can be evaluated by two methods:

(a) Dimensional Analysis combined with experimental investigations

(b) Analytical solution of momentum and energy equations 10 the boundary layer.

Dimensional Analysis and Its Limitations

Since the evaluation of convective heat transfer coefficient is quite complex, it is based on a combination of physical analysis and experimental studies. Experimental observations become necessary to study the influence of pertinent variables on the physical phenomena.

Dimensional analysis  is  a mathematical technique used in  reducing the number of

experiments to a minimum by determining an empirical relation connecting the relevant variables and in grouping the variables together in terms of dimensionless numbers. And, the method can only be applied after the pertinent variables controlling t he phenomenon are Identified and expressed In terms of the primary dimensions. (Table 1.1)

In natural convection heat transfer, the pertinent variables are: h, r, k, m, Cp, L, ( DT),

b and g. Buckingham p's method provides a systematic technique for arranging the variables in dimensionless numbers. It states that the number of dimensionless groups, p’s, required

describe a phenomenon involving 'n' variables is equal to the number of variables minus the number of primary dimensions 'm' in the problem.

In SI system of units, the number of primary dimensions are 4 and the number of variables for free convection heat transfer phenomenon are 9 and therefore, we should expect (9 - 4) = 5 dimensionless numbers. Since the dimension of the coefficient of volume expansion, beta, is

Deta-1 , one dimensionless number is obviously beta( Del T). The remaining variables are written in a

functional form:

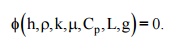
Since the number of primary dimensions are 4, we arbitrarily choose 4 independent variables as primary variables such that all the four dimensions are represented. The selected primary variables are: r,g, k. L Thus the dimensionless group,

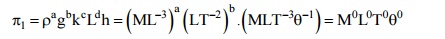
Equating the powers of M, L, T, Deta on both sides, we have

Up on solving them,:

M : a + c + 1 = 0 } Upon solving them,

L : -3a + b + c + d = 0

T : -2b -3c -3 = 0 q: -c - 1 = 0

c = 1, b = a = 0 and d = 1.

and values of the constant and 'm' are determined experimentally.

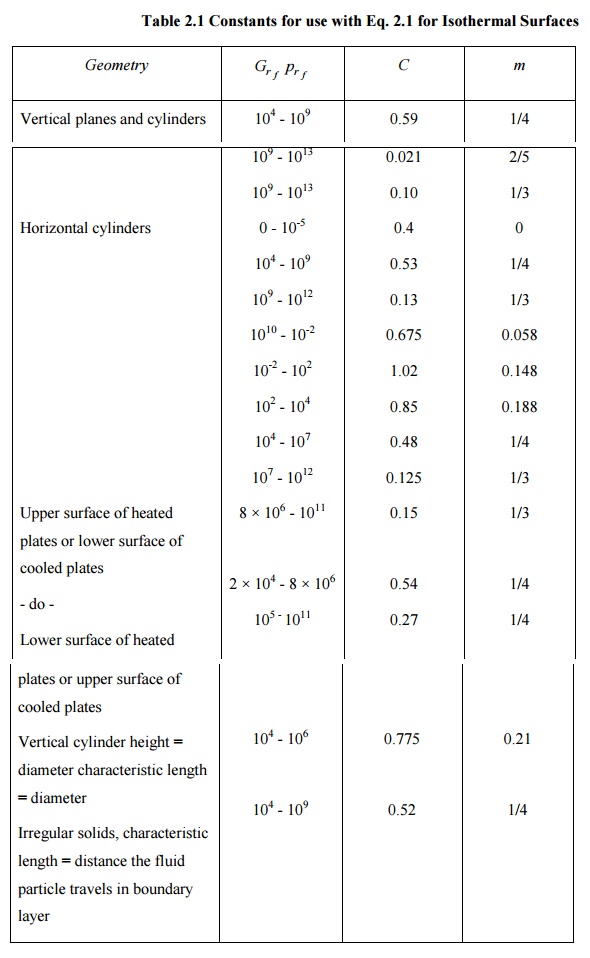
Table 2.1 gives the values of constants for use with Eq. (2.1) for isothermal surfaces.

Table 2.1 Constants for use with Eq. 2.1 for Isothermal Surfaces

Analytical Solution-Flow over a Heated Vertical Plate in Air

Let us consider a heated vertical plate in air, shown in Fig. 2.5. The plate is maintained at uniform temperature Tw .The coordinates are chosen in such a way that x - is in the streamwise direction and y - is in the transverse direction. There will be a thin layer of fluid adjacent to the hot surface of the vertical plate Within

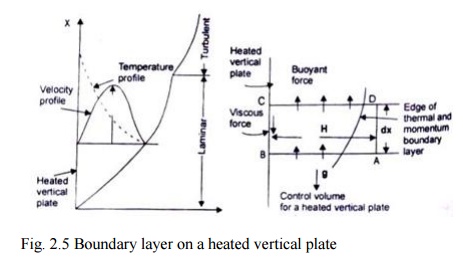
Fig. 2.5 Boundary layer on a heated vertical plate

which the variations in velocity and temperature would remain confined. The relative thickness of the momentum and the thermal boundary layer strongly depends upon the Prandtl number. Since in natural convection heat transfer, the motion of the fluid particles is caused by the temperature difference between the temperatures of the wall and the ambient fluid, the thickness of the two boundary layers are expected to be equal. When the temperature of the vertical plate is less than the fluid temperature, the boundary layer will form from top to bottom but the mathematical analysis will remain the same.

The boundary layer will remain laminar upto a certain length of the plate (Gr < 108) and beyond which it will become turbulent (Gr > 109). In order to obtain the analytical solution, the integral approach, suggested by von-Karman is preferred.

We choose a control volume ABCD, having a height H, length dx and unit thickness normal to the plane of paper, as shown in Fig. 25. We have:

(b) Conservation of Mass:

because the value of the integrand between dand H would be zero.

(iii) Conservation of Energy:

QAB ,convection + QAD ,convection + QBC ,conduction = QCD convection

Since the equations (2.2) and (2.3) are coupled equations, it is essential that the functional form of both the velocity and temperature distribution are known in order to arrive at a solution.

The functional relationship for velocity and temperature profiles which satisfy the above boundary conditions are assumed of the form:

After the Eqs. (5.4) and (5.5) are inserted in Eqs. (5.2) and (5.3) and the operations are performed (details of the solution are given in Chapman, A.J. Heat Transfer, Macmillan Company, New York), we get the expression for boundary layer thickness as:

Limitations of Analytical Solution: Except for the analytical solution for flow over a flat plate, experimental measurements are required to evaluate the heat transfer coefficient. Since in free convection systems, the velocity at the surface of the wall and at the edge of the boundary layer is zero and its magnitude within the boundary layer is so small. It is very difficult to measure them. Therefore, velocity measurements require hydrogen-bubble technique or sensitive hot wire anemometers. The temperature field measurement is obtained by interferometer.

Expression                 for   ‘h’   for   a   Heated   Vertical

The characteristic length used in evaluating the Nusselt number and Grashof number for vertical surfaces is the height of the surface. If the boundary layer thickness is not to large compared with the diameter of the cylinder, the convective heat transfer coefficient can be evaluated by the

equation used for vertical plane surfaces. That is, when D / L ³25/ (GrL )0.25

FLOW OVER CYLINDERS:

Laminar Flow Forced Convection Heat Transfer