Liquid-Liquid Extraction: Theory

THEORY

The behavioural pattern of two immiscible solvents, say ‘a’ and ‘b’, is essentially nonideal with respect to one another. Now, if a third substance is made to dissolve in a two-phase mixture of the solvents (i.e., ‘a’ and ‘b’), it may behave ideally in either phases provided its concentration in each individual phase is approximately small. Therefore, under these prevailing experimental parameters the ratio of the mole fractions of the solute in the two respective immiscible phases (‘a’ and ‘b’) is found to be a constant which is absolutely independent of the quantity of solute present. It is termed as the Nernst Distribution Law or the Partition Law and may be expressed as follows :

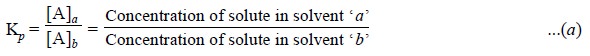
where, [A]_a = Mole fraction of solute A in Phase ‘a’

[B]_b = Mole fraction of solute B in Phase ‘b’, and

K_p = A constant.

The constant (K_p) is also known as the distribution coefficient or the partition coefficient. Interest-ingly, this particular relation [Eq. (a)] was originally derived for ideal solutions only, but it caters for a fairly good description of the behavioural pattern of a number of real-extraction-systems encountered in the analy-sis of pharmaceutical substances. However, the Partition Law offers the following two limitations, namely :

(a) It is not thermodynamically rigorous i.e., it takes no cognizance of the activities of the different species. In other words, it is solely applicable to very dilute solutions in which case the ratio of the activities almost approaches unity, and

(b) It does not hold good when the distributing substances encounters association or distribution in either phases (i.e., ‘a’ and ‘b’).

Consequently, a more rigorous treatment particularly specifies K_p as the ratio of the activities of the substance (A) in the two solvents instead of their concentrations. Hence, for dilute solutions, at a specified constant pressure and temperature, the mole fraction of a solute is directly proportional to its concentration in molarity or mass per unit volume ; which implies that these may be employed instead of mole-fraction in Eq. (a).

Thus, the Partition Coefficient K_p is also given by the following expression :

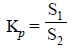                      ..............................(b)

where, S₁ = Solubility of substance A in solvent ‘a’, and

S₂ = Solubility of substance A in solvent ‘b’.

Adequate precaution and care must be exercised in determining partition coefficients based on the solubility data as S₁ is not the solubility of substance ‘A’ in pure Solvent ‘a’, but rather the solubility in Solvent ‘a’ saturated with Solvent ‘b’.

Example : In order to determine the exact partition coefficient of substance ‘A’ between water and ethyl acetate, the appropriate solubilities would be those of the substance ‘A’ in 3.3% ethyl acetate in water (composition of the ‘aqueous’ layer) and 8.7% in water in ethyl acetate (composition of the ‘ester’ layer).

Likewise, the following Table 27.1, records the mutual solubilities of a few typical solvent pairs that are used frequently for liquid-liquid extraction procedures.

In liquid-liquid extractions the following two aspects are very crucial and important, namely :

(a) Error due to the Volume Change, and

(b) Effectiveness of an Extraction.

These two aspects shall be discussed briefly at this juncture.

1. ERROR DUE TO THE VOLUME CHANGE

In a situation wherein two immiscible solvents are employed in an extraction, the volumes of the two individual phases after attainment of equilibrium may be appreciably different in comparison to the initial volumes of the solvents used. Therefore, a number of procedures have been adopted to avoid ‘error due to the volume change’ incurred thereby, namely :

(i) Measure the volume of the phase employed for the analysis and incorporate this volume in the calculations,

(ii) Separate the phase quantitatively and subsequently dilute to a known volume,

(iii) Separate the phase quantitatively and make use of the entire volume in the remaining steps of the ongoing analysis, and

(iv) Carry a marker substance through the extraction to automatically compensate for volume changes.

However, the latter procedure finds its abundant use in chromatographic methods of analysis.

2. EFFECTIVENESS OF AN EXTRACTION

Based on the appropriate partition coefficient of an immiscible solvent pair it is possible to calculate the ‘effectiveness of an extraction’.

Let us assume that ‘x’ moles of solute present initially in a volume V₂ of Solvent ‘b’. Now, this particular sample undergoes extraction with a volume V₁ of Solvent ‘a’ and subsequently ‘y’ moles of com-pound are left in V₂ at equilibrium.

Substituting these values in Eq. (a) and using molarity instead of mole fraction, we have :

after simplifying and rearranging :

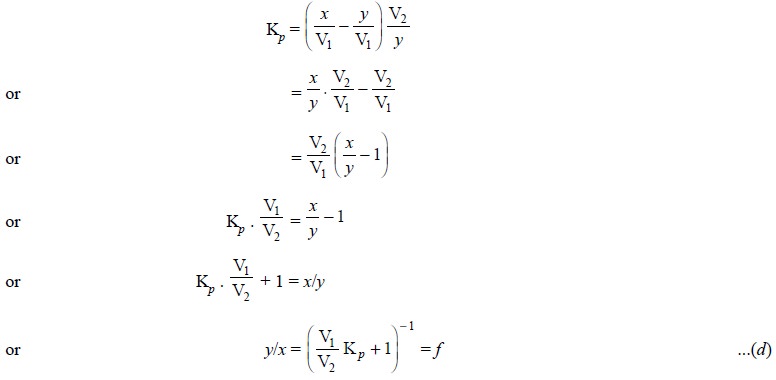
where, f = Fraction not extracted.

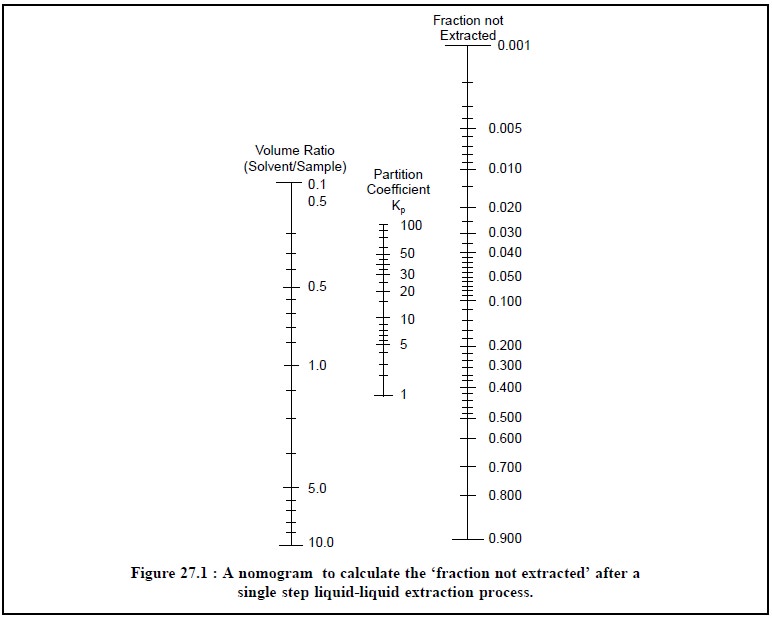
Figure 27.1, represents the nomogram from which the unextracted fraction for various values of V₂/V₁ and K may be obtained.

From Eqs. (d) it is quite evident that the fraction extracted is absolutely independent of the initial solute concentration. Hence, the fraction left unextracted after ‘n’ extraction may be given by the following expression:

              ..................................(e)

assuming that the same volumes of solvents have been used for each extraction.

Form Eq. (e) it is distinctly obvious that a series of several extractions would definitely prove to be more efficacious than one single extraction using the same total volume of solvent.

From figure 27.1, the following steps may be adopted in order to determine the percentage of the analyte left in the sample after a single extraction :

(i)          Hold a straight edge in such a manner that it is made to pass though the point on the ‘left scale’ which exactly corresponds to that ratio of extracting solvent to sample solvent volume and through the point representing the partition coefficient (K_p) on the ‘middle scale’, and

(ii)       The percentage of the ‘analyte’, left behind in the sample solvent after a single extraction is given by the intersection of the straight-edge with the ‘right scale’.