Life Table and Its Applications

Life Table and Its Applications

A Life Table is a presentation of summary of the mortality experiences of a community during a given period in the form of a table. The Life Table exhibits the number of persons living and dying at each age, on the basis of the experience of a cohort . It also gives the probability of dying and living separately. The Life Table tells the life history of a cohort.

Cohort is a group of individuals who born at the same time and experienced the same mortality conditions.

Uses of Life Table

·              Actuaries compute rate of premiums for persons of different age groups using Life Table.

·              It helps to assess the accuracy of census figures, death and birth registrations.

·              It helps to evaluate the impact of family planning on population growth.

·              It enables to assess the increase in the life span due to new scientific inventions, sophisticated medical treatments and improved living conditions.

·              Estimates of migration can be made from Life Table.

Construction of Life Table

Construction of Life Table begins with a cohort population. The following are the standard set of components of a Life Table:

(i) Age (x)

(ii) Survivorship function

(iii) Number of deaths in the age interval (x, x+1)

(iv) Probability for a person surviving at the age x to die before x+1 years

(v) Probability for a person aged x years to survive upto x+1 years

(vi) Number of persons lived in aggregate in the age interval (x,x+1)

(vii) Number of years lived by the cohort at and above the age x years

(viii) Expectation of life.

These components are described below with their respective notations and formula required to compute each of them.

(i) x : Age, in years

(ii) l(x): Number of survivors at the exact age of x years.

For instance, l(25) denotes the number of persons who survive to the moment of attaining age 25 years. Hence, l(x) is a decreasing function of x.

l(0) is called radix of the Life Table or cohort, which is conventionally taken as 1,00,000.

(iii) d(x): Number of persons among l(x) persons who die before reaching the age x years. i.e., d(x) = l(x) – l(x+1)

(iv) q(x): Probability for a person surviving at the age x will die before x+1 years. i.e., q(x) = d((x)) / l x

It is the proportion of persons dying between the ages of x and x +1 to the number of persons surviving at the age of x years, i.e., at the beginning of the corresponding age interval.

(v) p(x): Probability for a person aged x years to survive up to x+1 years

p(x) = 1 − q(x), or equivalently, p ( x) = l ( x +1) / l ( x)

It is the proportion of persons surviving up to (x + 1) years to the number of persons at the 

age of x years.

(vi) L(x): Number of persons lived in aggregate in the age interval (x,x+1)

i.e., L(x) = ^{l(x) + l(x + 1) / 2}

or equivalently

L ( x ) = l ( x ) –  1/2 d ( x)

(vii) T(x): Number of years lived by the cohort at and above the age x i.e., T(x) = L(x)+L(x+1)+L(x+2)+ ...

or equivalently

T(x+1) = T(x) – L(x).

Total number of years lived by the cohort after x years of age.

(viii) e⁰(x): Expectation of life

e ⁰( x) = T ( x) / l ( x)

It gives the average number of years a person of age x years is expected to survive under the existing mortality conditions.

Assumptions of Life Table

The following assumptions are made while constructing a Life Table.

(i) There is no effect of immigration and emigration on the cohort. It means that the reduction in the number of the initial cohorts is merely due to deaths.

(ii) The size of cohort begins with a convenient figure, it is conventionally 1,00,000.

(iii) Deaths are uniformly distributed over each age interval.

Example 8.6

A Life Table was constructed for a cohort. The following is a section of the table, wherein some of the entries are not available. Find the estimates of missing values and complete the Life Table.

Solution:

The Life Table can be completed using the relationship among missing terms and other terms.

The number of persons who die before reaching age 40 years is calculated as

d(40) = l(40) – l(41)

= 10645 – 10543

Therefore, d(40) = 102.

Values of q(x) are estimated as

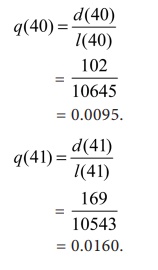
Values of p(x) are estimated from the corresponding values of q(x) as

p(40) = 1 – q(40)

= 1 – 0.0095 = 0.9905

p(41) = 1 – q(41)

= 1 – 0.0160 = 0.9840

Values of L(x) are estimated using its relationship with l(x) and d(x) as follows:

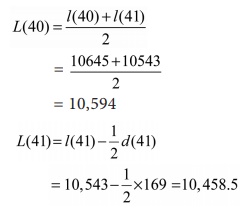
= 10,459 (Approx.)

The value of T(41) is estimated from the given value of T(40) and the estimated value of L(40) from the relationship

T(41) = T(40) – L(40)

as T(41) = 193820 – 10594

= 1,83,226.

The life expectancy of the cohort at the age x = 40 and 41 years can be estimated using the relationship

Now, the completed Life Table becomes as

Example 8.7

The following is a part of the Life Table constructed for a population, where the contents are incomplete. Evaluate the missing values using the given data and complete the Life Table.

Solution:

Values of the missing entries can be estimated from the given data applying the respective formulae as follows:

The number of persons who die before reaching age of 83 years is calculated as

d(83) = l(83) × q(83)

= 3560 × 0.16

= 569.6 = 570

The value of the survivorship function l(x) at x = 84 years is estimated as

l(84) = l(83) – d(83)

= 3560 – 570

= 2990

Values of p(x) are estimated from the corresponding values of q(x) as

p(83) = 1 – q(83)

= 1 – 0.16 = 0.84

p(84) = 1 – q(84)

= 1 – 0.17 = 0.83

Values of L(x) are estimated using its relationship with l(x) and d(x) as follows:

The value of T(83) can be estimated from the given value of T(84) and the estimated value of L(83) from the relationship

T(84) = T(83) – L(83)

T(83) = L(83) + T(84)

as

T(83) = 3,275 + 11975 = 15,250

The life expectancy of the cohort at the age x = 83 and 84 years is estimated using the relationship 

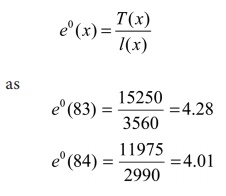
Now, the completed Life Table is as follows:

Example 8.8

A part of the Life Table of a population is given hereunder with incomplete information.

Find those information from the given data and complete the Life Table.

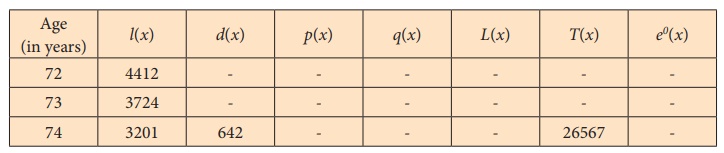
Solution:

Values of the missing entries can be calculated from the given data applying the respective formulae as follows:

The number of persons who die before reaching age x = 72 and 73 years can be calculated as d(72) = l(72) – l(73)

= 4412 – 3724

= 688

d(73) = l(73) – l(74)

= 3724 – 3201

d(73) = 523.

Values of q(x) are estimated as

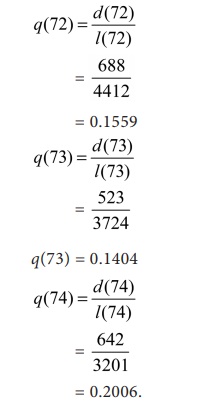
Values of p(x) are estimated from the corresponding values of q(x) as

p(72) = 1 – q(72)

= 1 – 0.1559 = 0.8441

p(73) = 1 – q(73)

= 1 – 0.1404 = 0.8596

p(74) = 1 – q(74)

= 1 – 0.2006 = 0.7994.

Values of L(x) are estimated using its relationship with l(x) and d(x) as follows:

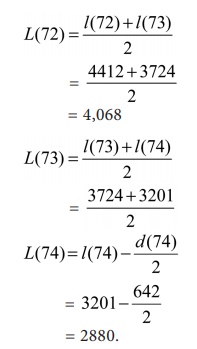
The value of T(x) is estimated for x = 72 and 73 from the given value of T(74) and the estimated values of L(72) and L(73) as

p(73) = L(73) + T(74)

= 3463 + 26567 = 30,030.

p(72) = L(72) + T(73)

4068 + 30030 = 34,098.

The life expectancy of the cohort at the age x = 72, 73 and 74 years is estimated using the relationship

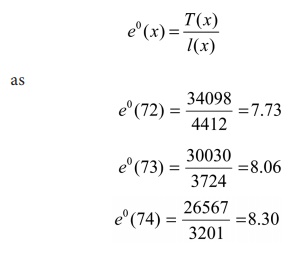
The completed Life Table is as follows:

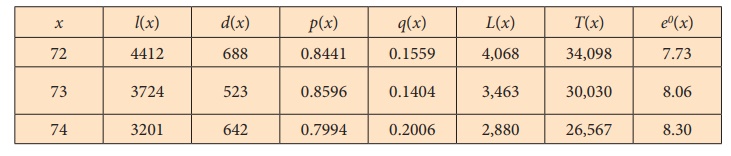
Example 8.9

Find the missing values in the following Life Table:

Solution:

Value of the survivorship function l(x) at x = 5 years can be estimated as

l(5) = l(4) – d(4)

= 95000 – 500

= 94500

Values of q(x) are estimated as

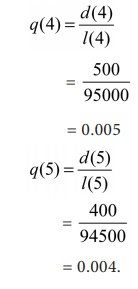
Values of p(x) are estimated from the corresponding values of q(x) as

p(4) = 1 – q(4)

= 1 – 0.005 = 0.995

p(5) = 1 – q(5)

= 1 – 0.004 = 0.996.

Values of L(x) are estimated using its relationship with l(x) and d(x) as follows:

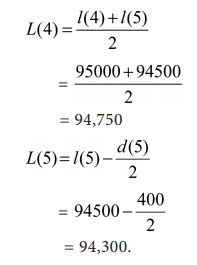
The value of T(5) is estimated from the given value of T(4) and the estimate of L(4) as

T(5) = T(4) – L(4)

T(5) = 4850300 – 94750 = 47,55,550.

The life expectancy of the cohort at the age x = 4 and 5 years is estimated using the relationship

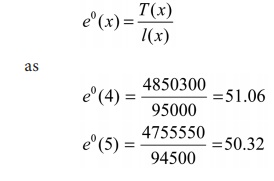
The completed Life Table is