Chapter: Engineering Mechanics : Basics and Statics of Particles
Laws of Mechanics
Laws of Mechanics
1 Newton’s law
Law I
Each body remains in its state of rest or motion uniform in direction until it is made to change this state by imposed forces.
Law II
The change of motion is proportional to the imposed driving force and occurs along a straight line in which the force acts.
Law III
To every action there is always an equal reaction: or the mutual interactions of two bodies are always equal but directed contrary.
2 Lami’s theorem
It states that, “If there forces acting at a point are in equilibrium, each force will be proportional to the sine of the angle between the other two forces.”
Suppose the three forces P, Q and Rare acting at a point 0 and they are in equilibrium as shown in Fig.
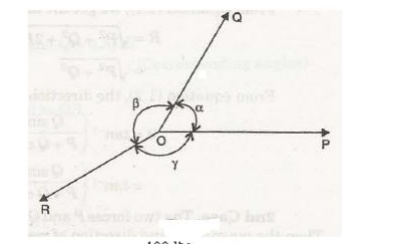
Let a = Angle between force P and Q.
β =Angle between force Q and R.
y = Angle between force R and P.
Then according to Lame’s theorem, P is proportional sine of angle between Q and R a sin β. P / sin β = constant.
Similarly Q / sin γ = constant,
R / sin a = constant P / sin β = Q / sin γ = R / sin a
Example-1: In a jib crane, the jib and the tie rod are 5 m and 4 m long resp ectively. the height of crane post in 3 m and the ti es red remains horizontal. Determine the for ces produced in jib and tie rod when a load of 2 kn in suspended at the crane head.
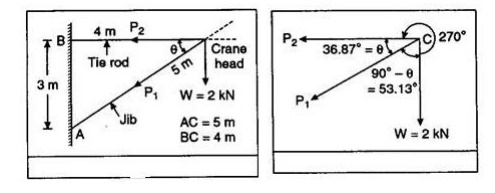
Solution: From figure
sin q = 3/5 = 0.6
q = 36.87o
Let P1 and P2 be the forces developed in jib and tie rod respectively. the three forces P1, P2 and W are shown in figure with the angle between the forces calculated from the given directions. The line of action of forces P1, P2 and weigh W meet at the point C, and therefore Lami’s theorem is
applicable. That gives:
∴P1/sin 270o = P2/sin 53.13o = 2/si n36.87o
P1 = 2 × sin 270 o / sin 36.87o = 2 × 1/0. = –3.33 kN
P2 = 2 × sin 53.13 o / sin 36.87o = 2 × 0.8 / 0.6 = 2.667 kN
The –ve sign indicates that the direction of force P1 is opposite to that shown in figure obviously the tie rod will be under tension and jib will in compression.
Examples-2: A string ABCD w hose extremity A is fixed has weights W1 and W2 attached to it at B and C, and passes round a smooth peg at D carrying a weight of 800 N at the free end E shown in Figure. If in a state of equilibrium, BC is horizontal and AB and CD make angles of 150o and 120o respectively wit h BC, make calculation for (a) The tension i n portion AB, BC, CD and DE of the string. (b) t he value of weights W1 and W2 (c) The load o n the peg at D
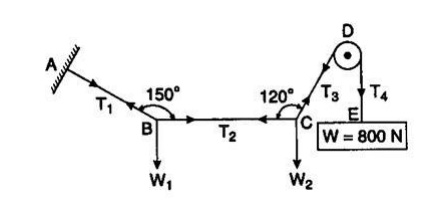
Solution: Let T1, T2, T3, T4 be the tension in segments AB, BC, CD and DE of the string.
Under equilibrium condition, T5 = T4 = 800 N
Applying Lami’s theorem at point B,
T1/sin90o = T2/sin120o = W1/sin150o
T1 = T2 sin 90o / sin 120o = 400 × 1/0.866 = 461.89 N
W1 = T2 sin 150o / sin 120o = 400 × 0.5 / 0.866 = 230.95 N
(c) Load on peg at D = T3 sin 60o + W
= 800 sin 60o + 800 = 692.82 + 800
= 1492.82 N
3 Parallelogram Law of forces
The law of parallelogram of forces is used to determine the resultant* of two forces acting at a point in a plane. It states, “If two forces, acting at a point be represented in magnitude and direction by the two adjacent sides of a parallelogram, then their resultant is represented in magnitude and direction by the diagonal of the parallelogram passing through that point.”
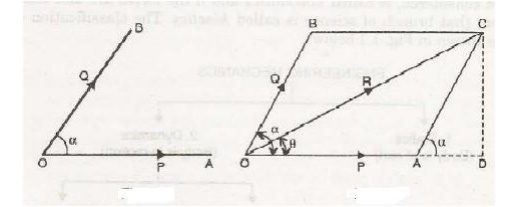
Let two forces P and Q act at a point 0 as shown in Fig. 1.3. The force P is represented in magnitude
and direction by OA whereas the force Q is presented in magnitude and direction by OB. Let the angle between the two forces be ‘a’. The resultant of these two forces will be obtained in magnitude
and direction by the diagonal (passing through O) of the parallelogram of which OA and OB are two adjacent sides. Hence draw the parallelogram with OA and OB as adjacent sides as shown in Fig. The resultant R is represented by OC in magnitude and direction.
Magnitude of Resultant (R)
From C draw CD perpendicular to OA produced.
Let a = Angle between two forces P and Q = LAOB
Now < DAC = < LAOB (Corresponding angles)
In parallelogram OACB, AC is parallel and equal to OB .
AC=Q.
In triangle ACD,
AD = AC cos a = Q cos a and CD =AC sin a= Q sin a.
In triangle OCD,
OC2 = OD2 + DC2.
But OC = R, OD = OA +AD = P + Q cos a and DC =Q sin a
R 2 = (P + Q cos a)2 + (Q sin a)2 = p2 + Q2 cos2 a+ 2PQ cos < X+ Q2 sin2 a
= p2 + Q2 (cos2 a+ sin2 a)+ 2PQ cos a
= P2 + Q2 + 2PQ cos a
R = √ p2 + Q2 + 2PQ cos a
Direction of Resultant
Let θ = Angle made by resultant with OA.
Then from triangle OCD,
tan θ = CD / OD = Q sin a / P + Q cos a θ = tan -1 ( Q sin a / P + Q cos a)
The direction of resultant can a lso be obtained by using sine rule [In triangle O AC, OA = P, AC = Q, OC = R, angle O AC = (180 - a), angle ACO = 180- [θ + 180 - a] = (a- θ)]
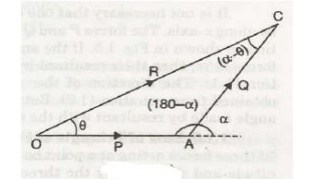
sin θ / AC = sin (180 –a) OC = sin (a – θ) / OA sin θ / Q = sin (180 – a) / R = sin (a – θ) / P
Two cases are important.
1st Case. If the two forces P and Q act at right angles, then a = 90° we get the m agnitude of resultant as
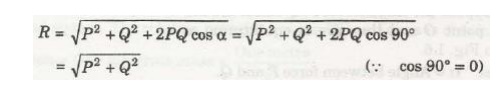
the direction of resultant is obtai ned as θ = tan -1 ( Q sin a / P + Q sin a)
= tan -1 ( Q sin 900 / P + Q cos 90 0 ) = tan -1 Q /P
2nd Case. The two forces P and Q are equal and are acting at an angle a betwee n them. Then the magnitude and direction of resul tant is given as

4 Law of Triangle of Forces
It states that, “if three fo rces acting at a point be represented in magnitude and direction by the three sides of a triangle, take n in order, they will be in equilibrium.”
5 Vectorial representation of forces
A force can be represented as a vector. Forces and vectors share three major characteristics:
v Magnitude
v Direction
v Location
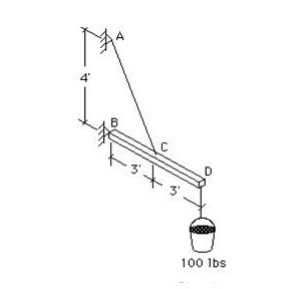
The simple support structure in Figure can be used to illustrate the three characteristics that make a force equivalent to a vector.
6 How Forces Are Represented
There are two ways in which forces can be represented in written form:
1. Scalar Notation
2. Vector Notation
3. The method used depends on the type of problem being solved and the easiest approach to finding a solution.
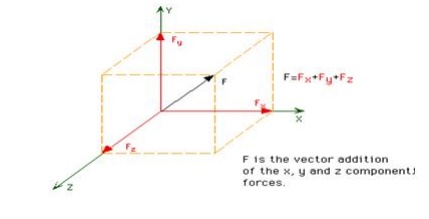
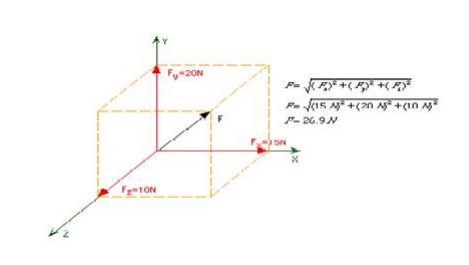
Scalar notation is useful when describing a force as a set of orthogonal force components. For example: Fx = 15N, Fy = 20N, Fz = 10N.
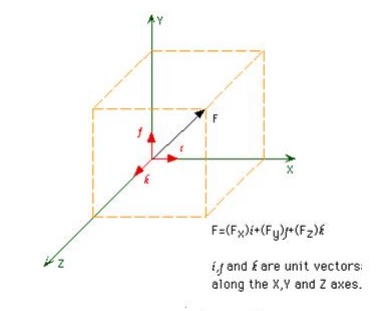
Vector notation is useful when vector mathematics are to be applied to a problem, such as addition or multiplication. Vector notation is somewhat simple in form:
F = 15i + 20j + 10k N.
The N term represents the unit of force, Newtons in this instance.
7 Addition of Forces
Multiple forces can be applied at a point. These forces are known as concurrent forces and can be added together to form a resultant force. If the component forces are orthogonal, then the magnitude of the resultant force can be determined by taking the Square Root of the Sum of the Squares (SRSS). The SRSS method is an extension of the Pythagorean Theorem to three dimensions.
8 Dot Product
Sometimes it is useful t o know how much of a force is acting in a dire ction other than the X,Y,or Z direction. Such a case might involve a bolted connection with a slotted hole, as shown in Figure.
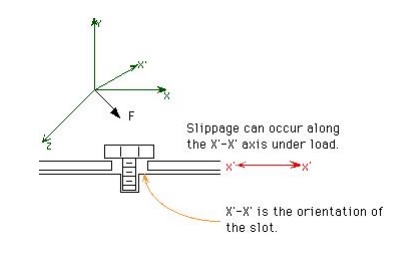
Suppose that the force i n Figure 1.5.1 was F=40i + 10j + 30kNewtons, and that the X' axis was oriented along the unit vect or e=0.6i + 0.5j - 0.624k. The projection of F onto X' would be the force component acting in the direction of the slot. Now consider the possibility that the connection would slip if Fx' was greater th an 35 N. Will the connection slip? The dot p roduct will help us answer this question.
9 Resultant of Three Force Vectors
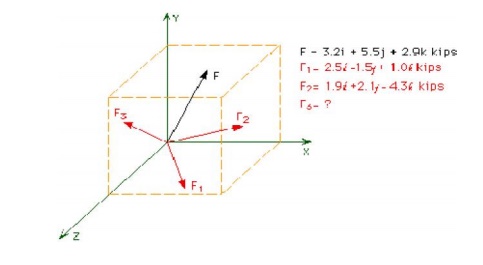
Three force vectors (F1, F2, F3) are simmultaneously applied at point A. The resultant of these three forces is F. Determin e F3 such that: F = 3.2i + 5.5j + 2.9k. Write F3 in vector notation.
10 Equation of equilibrium
A particle is in equilibrium if it is stationary or it moves uniformly relative to an inertial frame of reference. A body is in equilibrium if all the particles that may be considered to comprise the body are in equilibrium. One can study the equilibrium of a part of the body by isolating the part for analysis. Such a body is called a free body. We make a free body diagram and show all the forces from the surrounding that act on the body. Such a diagram is called a free-body diagram. For example, consider a ladder resting against a smooth wall and floor. The free body diagram of ladder is shown in the right. When a body is in equilibrium, the resultant of all forces acting on it is zero. Thus that resultant force R and the resultant couple M R are both zero, and we have the equilibrium equations
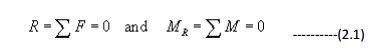
These requirements are necessary and sufficient conditions.
Let us understand equation for different type of force systems.
Types of system of forces 1. Collinear forces :
In this system, line of action of forces act along the same line is called collinear forces. For example consider a rope is being pulled by two players as shown in figure F1 F2
2. Coplanar forces
When all forces acting on the body are in the same plane the forces are coplanar
3. Coplanar Concurrent force system
A concurrent force system contains forces whose lines-of action meet at same one point. Forces may be tensile (pulling) or Forces may be compressive (pushing)

4. Non Concurrent Co-Planar Forces
A system of forces acting on the same plane but whose line of action does not pass through the same point is known as non concurrent coplanar forces or system for example a ladder resting against a wall and a man is standing on the rung but not on the center of gravity.
5. Coplanar parallel forces
When the forces acting on the body are in the same plane but their line of actions are parallel to each other known as coplanar parallel forces for example forces acting on the beams and two boys are sitting on the sea saw.
6. Non coplanar parallel forces
In this case all the forces are parallel to each other but not in the same plane,for example the force acting on the table when a book is kept on it.


11 Forces in Space
The resultant, R of two o r more forces in space is obtained by summing their rectangular components i.e.
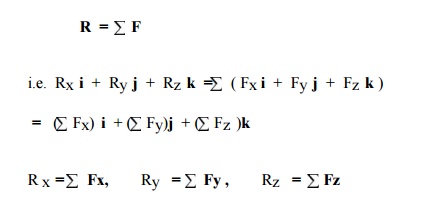
12 Equilibrium of a particl e in space
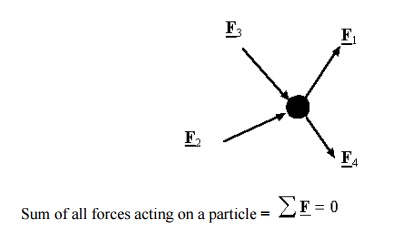
A particle is in equilibrium if the resultant of ALL forces acting on the particle is equal to zero
(Newton’s first law is that a bod y at rest is not subjected to any unbalanced force s).
Equilibrium equations in component form: In a rectangular coordinate system the equilibrium equations can be represented by three scalar equations:
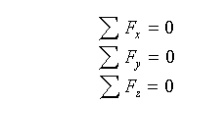
To apply equilibrium equations we must account for all known and unknown forces acting on the particle. The best way to do this is to draw a free-body diagram of the particle.
13 The principle of transmissibility
If a force, acting at a point on a rigid body, is shifted to any other point which is on the line of action of the force, the external effect of the force on the body remains unchanged".
14 Single Equivalent Force
When a number of forces are acting on a rigid body, then these forces can be replaced by a single force which has. the same effect on the rigid body as that of all the forces acting together, then this single, force is known as 'Single Equivalent Force'. This single equivalent force is also known as resultant of several forces. Hence a single force which can replace a number of forces acting on a rigid body, without causing any change in external effects on the body, is known as single equivalent force (or resultant force )
Related Topics