Equilibrium of Rigid Bodies

EQUILIBRIUM OF RIGID BODIES

Free body Diagram

A diagram of a body (or a part of it) which shows all the forces and couples applied on it, and which has all the forces and couples labeled for use in the solution of the problem is called a free-body diagram. Follow these steps to draw a free-body diagram.

1. Select the body (or  part of a body) that you want to analyze, and draw it.

2. Identify all the forces and couples that are applied onto the body and draw them on the body. Place each force and couple at the point that it is applied.

3. Label all the forces and couples with unique labels for use during the solution process.

4. Add any relevant dimensions onto your picture.

1.Forces and couples on a free-body diagram

Each force or couple you put on a free-body diagram represents a model of how the body in the free-body diagram is effected by its surroundings. In selecting the forces and couples that are to be applied on the free-body diagram follow these steps:

1.  Identify all the forces which come from the interaction of one body with another. Many of the common supports and their effects are shown in Table 5-1 on page 184. Remember that for each way in which a support restricts the free motion of the body, a force or a moment must be applied to the body to impose the restriction on the motion.

2. Apply the weight of the body to its center of gravity (if it is uniform, then apply it to the centroid).

3. Remember that strings and cables can only pull on an object.

4. Remember that internal loads cancel out and should not be put on the free-body diagram.

5 Remember that if you have selected the direction of forces or couples of interaction on one body, then Newton’s 3^rd law states that you must apply the forces or couples in the opposite direction on

the other body.

Types of supports and their reactions

Types of reaction and its direction will depend upon the type of support provided.

1.Friction less or smooth surface support

2.Roller support

3.Knife edge support

4.Hinged or pinnrd support

5.Fixed or built in support

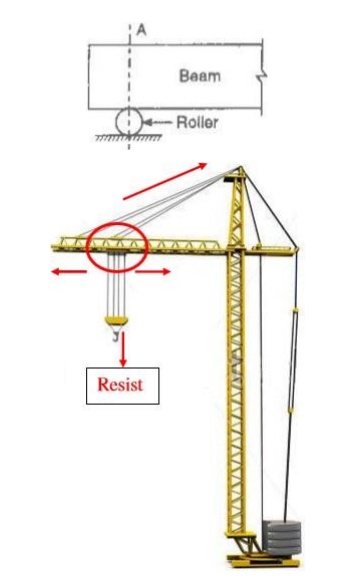
1 Roller Supports

Roller supports are free to rotate and translate along the surface upon which the roller rests. The surface may be horizontal, vertical or slopped at any angle. Roller supports are commonly located at one end of long bridges in the form of bearing pads. This support allows bridge structure to expand and contract with temperature changes and without this expansion the forces can fracture the supports at the banks. This support cannot provide resistance to lateral forces. Roller support is also used in frame cranes in heavy industries as shown in figure, the support can move towards left, right and rotate by resisting vertical loads thus a heavy load can be shifted from one place to another horizontally

2 Hinge Supports

The hinge support is capable of resisting forces acting in any direction of the plane. This support does not provide any resistance to rotation. The horizontal and vertical component of reaction can be determined using equation of equilibrium. Hinge support may also be used in three hinged arched bridges at the banks supports while at the center internal hinge is introduced. It is also used in doors to produce only rotation in a door. Hinge support reduces sensitivity to earthquake.

3 Fixed Support

Fixed support can resist vertical and horizontal forces as well as moment since they restrain both rotation and translation. They are also known as rigid support For the stability of a structure there should be one fixed support. A flagpole at concrete base is common example of fixed support In RCC structures the steel reinforcement of a beam is embedded in a column to produce a fixed support as shown in above image. Similarly all the riveted and welded joints in steel structure are the examples of fixed supports Riveted connection are not very much common now a days due to the introduction of bolted joints.

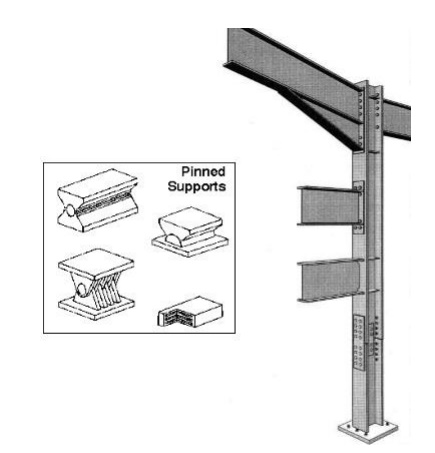
4 Pinned Supports

A pinned support is same as hinged support. It can resist both vertical and horizontal forces but not a moment. It allows the structural member to rotate, but not to translate in any direction. Many connections are assumed to be pinned connections even though they might resist a small amount of moment in reality. It is also true that a pinned connection could allow rotation in only one direction; providing resistance to rotation in any other direction. In human body knee is the best example of hinged support as it allows rotation in only one direction and resists lateral movements. Ideal pinned and fixed supports are rarely found in practice, but beams supported on walls or simply connected to other steel beams are regarded as pinned. The distribution of moments and shear forces is influenced by the support condition.

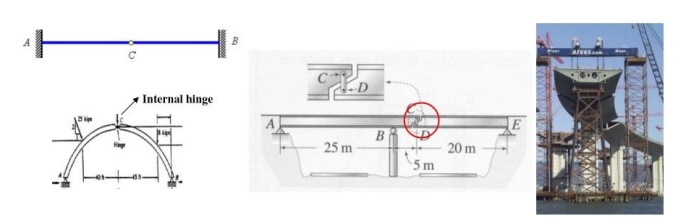
5 Internal Hinge

Interior hinges are often used to join flexural members at points other than supports. For example in above fig two halves of an arch is joined with the help of internal hinge.In some cases it is intentionally introduced so that excess load breaks this weak zone rather than damaging other structural elements as shown in above image.

Moments

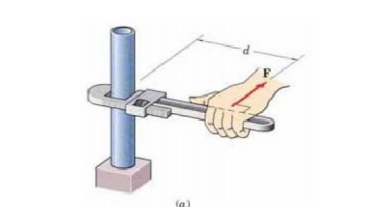
The tendency of a force to move the body in the direction of its application a force can tend to rotate a body about an axis. This axis may be any line which is neither intersects nor parallel to the line of the action of the force. This rational tendency of force is know as the moment of force. As a familiar example of the concept of moment, consider the pipe wrench as shown in figure (a). One effect of the force applied perpendicular to the handle of the wrench is the tendency to rotate the pipe about its vertical axis. The magnitude of this tendency depends on both the magnitude of the force and the effective length d of the wrench handle.Common experience shown that a pull which is not perpendicular to the wrench handle is less effective than the right angle pull. Mathematically this tendency of force (moment) is calculated by multiplying force to the moment

1 Moment about a point

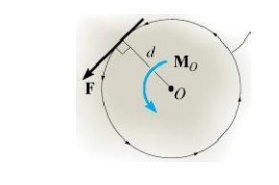
Consider following body (two dimensional) acted by a force F in its plane. The magnitude of moment or tendency of the force to rotate the body about the axis O_O perpendicular to the plane of the body is proportional both to the magnitude of the force and to the moment arm d, therefore magnitude of the moment is defined as the product of force and moment arm.

Moment = Force x moment arm

M = Fd

Where d = moment arm and F = magnitude of force

Moment arm is defined as the perpendicular distance between axis of rotation and the line of action of force.

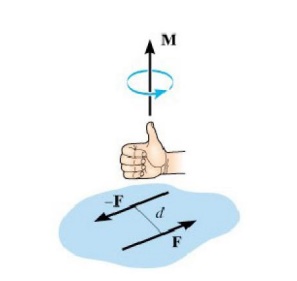
2 Direction of moment of a force

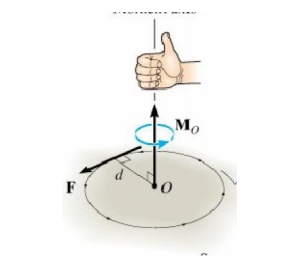
The direction Mo is specified using the “right-hand rule”. To do this the fingers of the right hand are curled such that they follow the sense of rotation, which would occur if the force could rotate about point O. The thumb then point along the moment axis so that it gives the direction and sense of the moment vector, which is upward and perpendicular to the shaded plane containing F and d.

3 Clock Wise And Anti Clock Wise Moments

The moment are classified as clockwise and anticlockwise moment according to the direction in which the force tends to rotate the body about a fixed point

Clockwise Moment

When the force tends to rotate the body in the same direction in which the hands of clock move is called clockwise moment the clockwise moment is taken as positive or other wise mentioned.

Anticlockwise Moment

When the force tends to rotate the body in the opposite direction in which the hands of clock move is called anti clockwise moment which is taken as negative or otherwise mentioned.

4 Unit of moment

S.I unit is N.m. (Newton. meter)

F.P.S unit is lb. ft (Pound. foot)

G.G.S unit is dyne.cm (dyne. Centimeter) etc

Example 1: Determine the moment of the force about point “O” for following diagram.

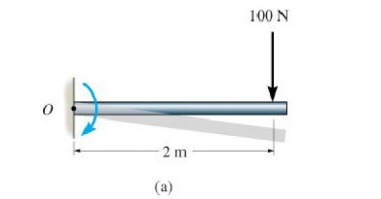
Given Force=100 N

Moment arm=2m

Required Mo=?

Working formula: - MO=Force x Moment arm.

Sol putt the values in first w, f

Mo= F x r = 100 x 2

Mo= 200N.m.

Result: - Moment = 200N.m Direction =Clock wise

Example 2: Determine the moment of the force 800 N acting on the frame about points A, B, C and D.

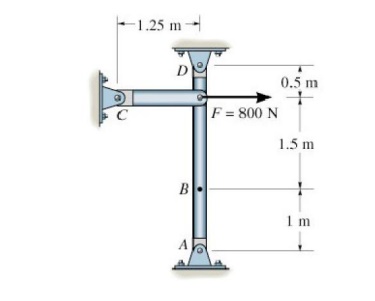
Given

Force = F = 800 N

Required MA=? MB? MC=? MD=?

Working formula

Moment =force x moment arm. Sol Solve this question step by step Now first consider the Point A. MA = F x r

MA = 800 x (1.5+1)

MA = 2000 N.m clock wise_______ I Now Moment about B

MB = F x r = 800x 5

MB = 1200 N m clock wise________ (2)

From (1) and (2) it is evidence that when force remain constant then moment varies with moment arm that is moment depends upon moment arm. Similarly it can be proved that moment about any point varies with force when moment arm remain same.

Now consider point C Moment = Force x distance Mc = 800 x 0

Mc = 0. _______ (3)

As the line of action of force passes through point C

that is point of application it shows that the line of action should be perpendicular to the point i.e. “C”

Now consider the point D. MD = F x r.

MD = 800 x 0.5 MD= 400 N.m

Result

MA =2000 N.m clock wise Or

MA = + 200 N.m

MB = 1200 N.m clock wise Or

MB = + 1200 N.m

MC = O.

Mc = O

MD =. 400 N.m anti clock wise

MD = - 400N.m

4 Principle of Moment/ Varignon’s Theorem

It is stated that the moment of a force about a point is equal to the sum of the moments of the force components about the point. Or the moment produce by the resultant force is equal to the moment produce by the force components.

Mathematically MFo = Σ Mo

Example 3: A 200 N force acts on the bracket as shown determine the moment of force about “A”

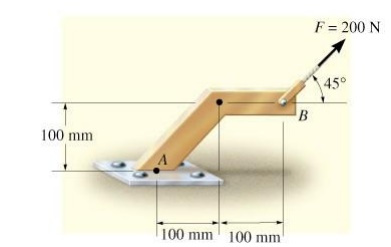
Given F=200N θ = 45º

Required MA =?

Solution Resolve the force into components F1 am F2

F1= F cos θ F1=200 cosine 45º

F1=141.42N.

F2= F sin θ F2 = 200 sin 45º

F2= 2.468N.

We know that MA = 0

MA = moment produce due to component F1+ moment produce due to component F2.

MA =F1 x r1+ F2 x r2.

Let us consider that clock wise moment is + ve. MA = F1 x r1+ F2 x r2

MA = - 141.42 x 0.1 + 2.468 x (0.1 +0.1) MA = - 13.648 N

MA = 13 .648 N anti clock wise.

 Couple

When two parallel forces that have the same magnitude but opposite direction is known as couple. The couple is separated by perpendicular distance. As matter of fact a couple is unable to produce any straight-line motion but it produces rotation in the body on which it acts. So couple can be defined as unlike parallel forces of same magnitude but opposite direction which produce rotation about a specific direction and whose resultant is zero

1 Application of Couple

1. To open or close the valves or bottle head, tap etc

2. To wind up a clock.

3. To Move the paddles of a bicycle

4. Turning a key in lock for open and closing.

2 Couple Arm

The perpendicular distance between the lines of action of the two and opposite parallel forces is known as arm of the couple.

3 Moment of couple or couple moment

The moment of the couple is the product of the force (one of the force of the two equal and opposite parallel forces) and the arm of the couple. Mathematically

Moment of couple = force x arm of couple Moment of couple = F x r

4 Direction of couple

The direction and sense of a couple moment is determined using the right hand rule, here the thumb indicates the direction when the fingers are curled with the sense of rotation caused by the two forces.

5 Classification of Couple

The couplet are classified as clockwise couple and anticlockwise couple

1. Clockwise couple

A couple whose tendency is to rotate the body in a clockwise direction is known as clockwise couple

2. Anticlockwise couple

A couple whose tendency is to rotate the body in anticlockwise direction is known as anticlockwise couple

Example 4: Determine the moment of couple acting on the moment shown.

GivenF1=F2 =90lb F3 = F4 = 120lb.

Required Moment of couple = M=?

Solution The moment of couple can be determined at any point for example at A, B or D.

Let us take the moment about point B

MB = Σ F R.

MB = -F1 x r1 – F2 x r2 .

MB = - 90(3) – 120 (1)

MB = - 390 lb ft

Result MB = MA=MD =390 lb .ft counter clock wise.

Moment of couple = 390 lb.ft count clock wise