Chapter: Introduction to the Design and Analysis of Algorithms : Space and Time Trade-Offs
Input Enhancement in String Matching: HorspoolŌĆÖs and Boyer-Moore Algorithm
Input Enhancement in String Matching
In this section, we see how the technique of input enhancement can be applied to the problem of string matching. Recall that the problem of string matching requires finding an occurrence of a given string of m characters called the pattern in a longer string of n characters called the text. We discussed the brute-force algorithm for this problem in Section 3.2: it simply matches corresponding pairs of characters in the pattern and the text left to right and, if a mismatch occurs, shifts the pattern one position to the right for the next trial. Since the maximum number of such trials is n ŌłÆ m + 1 and, in the worst case, m comparisons need to be made on each of them, the worst-case efficiency of the brute-force algorithm is in the O(nm) class. On average, however, we should expect just a few comparisons before a patternŌĆÖs shift, and for random natural-language texts, the average-case efficiency indeed turns out to be in O(n + m).
Several faster algorithms have been discovered. Most of them exploit the input-enhancement idea: preprocess the pattern to get some information about it, store this information in a table, and then use this information during an actual search for the pattern in a given text. This is exactly the idea behind the two best-known algorithms of this type: the Knuth-Morris-Pratt algorithm [Knu77] and the Boyer-Moore algorithm [Boy77].
The principal difference between these two algorithms lies in the way they compare characters of a pattern with their counterparts in a text: the Knuth-Morris-Pratt algorithm does it left to right, whereas the Boyer-Moore algorithm does it right to left. Since the latter idea leads to simpler algorithms, it is the only one that we will pursue here. (Note that the Boyer-Moore algorithm starts by aligning the pattern against the beginning characters of the text; if the first trial fails, it shifts the pattern to the right. It is comparisons within a trial that the algorithm does right to left, starting with the last character in the pattern.)
Although the underlying idea of the Boyer-Moore algorithm is simple, its actual implementation in a working method is less so. Therefore, we start our discussion with a simplified version of the Boyer-Moore algorithm suggested by R. Horspool [Hor80]. In addition to being simpler, HorspoolŌĆÖs algorithm is not necessarily less efficient than the Boyer-Moore algorithm on random strings.
HorspoolŌĆÖs Algorithm
Consider, as an example, searching for the pattern BARBER in some text:

Starting with the last R of the pattern and moving right to left, we compare the corresponding pairs of characters in the pattern and the text. If all the patternŌĆÖs characters match successfully, a matching substring is found. Then the search can be either stopped altogether or continued if another occurrence of the same pattern is desired.
If a mismatch occurs, we need to shift the pattern to the right. Clearly, we would like to make as large a shift as possible without risking the possibility of missing a matching substring in the text. HorspoolŌĆÖs algorithm determines the size of such a shift by looking at the character c of the text that is aligned against the last character of the pattern. This is the case even if character c itself matches its counterpart in the pattern.
In general, the following four possibilities can occur.
Case 1 If there are no cŌĆÖs in the patternŌĆöe.g., c is letter S in our exampleŌĆö we can safely shift the pattern by its entire length (if we shift less, some character of the pattern would be aligned against the textŌĆÖs character c that is known not to be in the pattern):
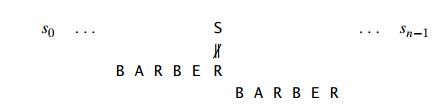
Case 2 If there are occurrences of character c in the pattern but it is not the last one thereŌĆöe.g., c is letter B in our exampleŌĆöthe shift should align the rightmost occurrence of c in the pattern with the c in the text:
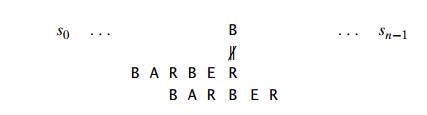
Case 3 If c happens to be the last character in the pattern but there are no cŌĆÖs among its other m ŌłÆ 1 charactersŌĆöe.g., c is letter R in our exampleŌĆöthe situation is similar to that of Case 1 and the pattern should be shifted by the entire patternŌĆÖs length m:

Case 4 Finally, if c happens to be the last character in the pattern and there are other cŌĆÖs among its first m ŌłÆ 1 charactersŌĆöe.g., c is letter R in our exampleŌĆö the situation is similar to that of Case 2 and the rightmost occurrence of c among the first m ŌłÆ 1 characters in the pattern should be aligned with the textŌĆÖs c:
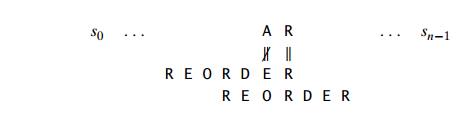
These examples clearly demonstrate that right-to-left character comparisons can lead to farther shifts of the pattern than the shifts by only one position always made by the brute-force algorithm. However, if such an algorithm had to check all the characters of the pattern on every trial, it would lose much of this superiority. Fortunately, the idea of input enhancement makes repetitive comparisons unnecessary. We can precompute shift sizes and store them in a table. The table will be indexed by all possible characters that can be encountered in a text, including, for natural language texts, the space, punctuation symbols, and other special characters. (Note that no other information about the text in which eventual searching will be done is required.) The tableŌĆÖs entries will indicate the shift sizes computed by the formula

For example, for the pattern BARBER, all the tableŌĆÖs entries will be equal to 6, except for the entries for E, B, R, and A, which will be 1, 2, 3, and 4, respectively.
Here is a simple algorithm for computing the shift table entries. Initialize all the entries to the patternŌĆÖs length m and scan the pattern left to right repeating the following step m ŌłÆ 1 times: for the j th character of the pattern (0 Ōēż j Ōēż m ŌłÆ 2), overwrite its entry in the table with m ŌłÆ 1 ŌłÆ j , which is the characterŌĆÖs distance to the last character of the pattern. Note that since the algorithm scans the pattern from left to right, the last overwrite will happen for the characterŌĆÖs rightmost occurrenceŌĆöexactly as we would like it to be.
ALGORITHM ShiftTable(P [0..m ŌłÆ 1])
//Fills the shift table used by HorspoolŌĆÖs and Boyer-Moore algorithms //Input: Pattern P [0..m ŌłÆ 1] and an alphabet of possible characters //Output: Table[0..size ŌłÆ 1] indexed by the alphabetŌĆÖs characters and // filled with shift sizes computed by formula (7.1)
for i ŌåÉ 0 to size ŌłÆ 1 do Table[i] ŌåÉ m
for j ŌåÉ 0 to m ŌłÆ 2 do Table[P [j ]] ŌåÉ m ŌłÆ 1 ŌłÆ j return Table
Now, we can summarize the algorithm as follows:
HorspoolŌĆÖs algorithm
Step 1 For a given pattern of length m and the alphabet used in both the pattern and text, construct the shift table as described above.
Step 2 Align the pattern against the beginning of the text.
Step 3 Repeat the following until either a matching substring is found or the pattern reaches beyond the last character of the text. Starting with the last character in the pattern, compare the corresponding characters in the pattern and text until either all m characters are matched (then stop) or a mismatching pair is encountered. In the latter case, retrieve the entry t (c) from the cŌĆÖs column of the shift table where c is the textŌĆÖs character currently aligned against the last character of the pattern, and shift the pattern by t (c) characters to the right along the text.
Here is pseudocode of HorspoolŌĆÖs algorithm.
ALGORITHM HorspoolMatching(P [0..m ŌłÆ 1], T [0..n ŌłÆ 1])
//Implements HorspoolŌĆÖs algorithm for string matching //Input: Pattern P [0..m ŌłÆ 1] and text T [0..n ŌłÆ 1]
//Output: The index of the left end of the first matching substring
or ŌłÆ1 if there are no matches
ShiftTable(P [0..m ŌłÆ 1]) //generate Table of shifts
i ŌåÉ m ŌłÆ 1 //position of the patternŌĆÖs right end
while i Ōēż n ŌłÆ 1 do
k ŌåÉ 0 //number of matched characters
while k Ōēż m ŌłÆ 1 and P [m ŌłÆ 1 ŌłÆ k] = T [i ŌłÆ k] do k ŌåÉ k + 1
if k = m
return i ŌłÆ m + 1 else i ŌåÉ i + Table[T [i]]
return ŌłÆ1
EXAMPLE As an example of a complete application of HorspoolŌĆÖs algorithm, consider searching for the pattern BARBER in a text that comprises English letters and spaces (denoted by underscores). The shift table, as we mentioned, is filled as follows:
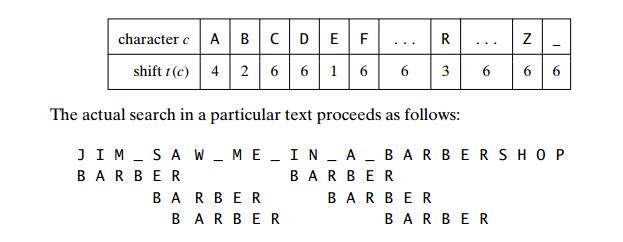
A simple example can demonstrate that the worst-case efficiency of Hor-spoolŌĆÖs algorithm is in O(nm) (Problem 4 in this sectionŌĆÖs exercises). But for random texts, it is in (n), and, although in the same efficiency class, HorspoolŌĆÖs algorithm is obviously faster on average than the brute-force algorithm. In fact, as mentioned, it is often at least as efficient as its more sophisticated predecessor discovered by R. Boyer and J. Moore.
Boyer-Moore Algorithm
Now we outline the Boyer-Moore algorithm itself. If the first comparison of the rightmost character in the pattern with the corresponding character c in the text fails, the algorithm does exactly the same thing as HorspoolŌĆÖs algorithm. Namely, it shifts the pattern to the right by the number of characters retrieved from the table precomputed as explained earlier.
The two algorithms act differently, however, after some positive number k (0 < k < m) of the patternŌĆÖs characters are matched successfully before a mismatch is encountered:
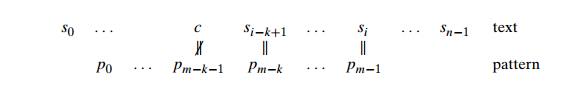
In this situation, the Boyer-Moore algorithm determines the shift size by consid-ering two quantities. The first one is guided by the textŌĆÖs character c that caused a mismatch with its counterpart in the pattern. Accordingly, it is called the bad-symbol shift. The reasoning behind this shift is the reasoning we used in Hor-spoolŌĆÖs algorithm. If c is not in the pattern, we shift the pattern to just pass this c in the text. Conveniently, the size of this shift can be computed by the formula t1(c) ŌłÆ k where t1(c) is the entry in the precomputed table used by HorspoolŌĆÖs algorithm (see above) and k is the number of matched characters:
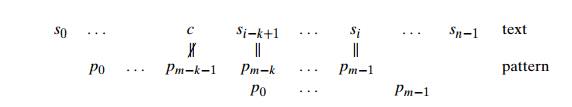
For example, if we search for the pattern BARBER in some text and match the last two characters before failing on letter S in the text, we can shift the pattern by t1(S) ŌłÆ 2 = 6 ŌłÆ 2 = 4 positions:

The same formula can also be used when the mismatching character c of the text occurs in the pattern, provided t1(c) ŌłÆ k > 0. For example, if we search for the pattern BARBER in some text and match the last two characters before failing on letter A, we can shift the pattern by t1(A) ŌłÆ 2 = 4 ŌłÆ 2 = 2 positions:
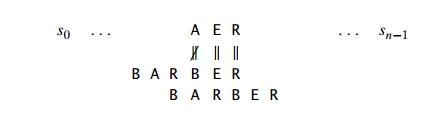
If t1(c) ŌłÆ k Ōēż 0, we obviously do not want to shift the pattern by 0 or a negative number of positions. Rather, we can fall back on the brute-force thinking and simply shift the pattern by one position to the right.
To summarize, the bad-symbol shift d1 is computed by the Boyer-Moore algorithm either as t1(c) ŌłÆ k if this quantity is positive and as 1 if it is negative or zero. This can be expressed by the following compact formula:

The second type of shift is guided by a successful match of the last k > 0 characters of the pattern. We refer to the ending portion of the pattern as its suffix of size k and denote it suff (k). Accordingly, we call this type of shift the good-suffix shift. We now apply the reasoning that guided us in filling the bad-symbol shift table, which was based on a single alphabet character c, to the patternŌĆÖs suffixes of sizes 1, . . . , m ŌłÆ 1 to fill in the good-suffix shift table.
Let us first consider the case when there is another occurrence of suff (k) in the pattern or, to be more accurate, there is another occurrence of suff (k) not preceded by the same character as in its rightmost occurrence. (It would be useless to shift the pattern to match another occurrence of suff (k) preceded by the same character because this would simply repeat a failed trial.) In this case, we can shift the pattern by the distance d2 between such a second rightmost occurrence (not preceded by the same character as in the rightmost occurrence) of suff (k) and its rightmost occurrence. For example, for the pattern ABCBAB, these distances for k = 1 and 2 will be 2 and 4, respectively:

What is to be done if there is no other occurrence of suff (k) not preceded by the same character as in its rightmost occurrence? In most cases, we can shift the pattern by its entire length m. For example, for the pattern DBCBAB and k = 3, we can shift the pattern by its entire length of 6 characters:

Unfortunately, shifting the pattern by its entire length when there is no other occurrence of suff (k) not preceded by the same character as in its rightmost occurrence is not always correct. For example, for the pattern ABCBAB and k = 3, shifting by 6 could miss a matching substring that starts with the textŌĆÖs AB aligned with the last two characters of the pattern:
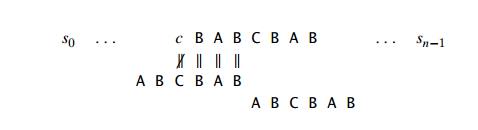
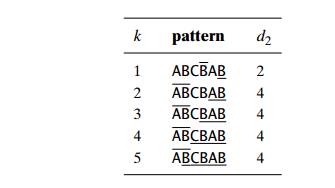
Note that the shift by 6 is correct for the pattern DBCBAB but not for ABCBAB, because the latter pattern has the same substring AB as its prefix (beginning part of the pattern) and as its suffix (ending part of the pattern). To avoid such an erroneous shift based on a suffix of size k, for which there is no other occurrence in the pattern not preceded by the same character as in its rightmost occurrence, we need to find the longest prefix of size l < k that matches the suffix of the same size l. If such a prefix exists, the shift size d2 is computed as the distance between this prefix and the corresponding suffix; otherwise, d2 is set to the patternŌĆÖs length m. As an example, here is the complete list of the d2 valuesŌĆöthe good-suffix table of the Boyer-Moore algorithmŌĆöfor the pattern ABCBAB:
Now we are prepared to summarize the Boyer-Moore algorithm in its entirety.
The Boyer-Moore algorithm
Step 1 For a given pattern and the alphabet used in both the pattern and the text, construct the bad-symbol shift table as described earlier.
Step 2 Using the pattern, construct the good-suffix shift table as described earlier.
Step 3 Align the pattern against the beginning of the text.
Step 4 Repeat the following step until either a matching substring is found or the pattern reaches beyond the last character of the text. Starting with the last character in the pattern, compare the corresponding characters in the pattern and the text until either all m character pairs are matched (then stop) or a mismatching pair is encountered after k Ōēź 0 character pairs are matched successfully. In the latter case, retrieve the entry t1(c) from the cŌĆÖs column of the bad-symbol table where c is the textŌĆÖs mismatched character. If k > 0, also retrieve the corresponding d2 entry from the good-suffix table. Shift the pattern to the right by the number of positions computed by the formula

Shifting by the maximum of the two available shifts when k > 0 is quite log-ical. The two shifts are based on the observationsŌĆöthe first one about a textŌĆÖs mismatched character, and the second one about a matched group of the patternŌĆÖs rightmost charactersŌĆöthat imply that shifting by less than d1 and d2 characters, re-spectively, cannot lead to aligning the pattern with a matching substring in the text. Since we are interested in shifting the pattern as far as possible without missing a possible matching substring, we take the maximum of these two numbers.
EXAMPLE As a complete example, let us consider searching for the pattern BAOBAB in a text made of English letters and spaces. The bad-symbol table looks as follows:

The actual search for this pattern in the text given in Figure 7.3 proceeds as follows. After the last B of the pattern fails to match its counterpart K in the text, the algorithm retrieves t1(K) = 6 from the bad-symbol table and shifts the pat-tern by d1 = max{t1(K) ŌłÆ 0, 1} = 6 positions to the right. The new try successfully matches two pairs of characters. After the failure of the third comparison on the space character in the text, the algorithm retrieves t1( ) = 6 from the bad-symbol table and d2 = 5 from the good-suffix table to shift the pattern by max{d1, d2} = max{6 ŌłÆ 2, 5} = 5. Note that on this iteration it is the good-suffix rule that leads to a farther shift of the pattern.
![]()
The next try successfully matches just one pair of BŌĆÖs. After the failure of the next comparison on the space character in the text, the algorithm retrieves t1( ) = 6 from the bad-symbol table and d2 = 2 from the good-suffix table to shift

the pattern by max{d1,d2} = max {6 ŌłÆ 1, 2} = 5. Note that on this iteration it is the bad-symbol rule that leads to a farther shift of the pattern. The next try finds a matching substring in the text after successfully matching all six characters of the pattern with their counterparts in the text.
When searching for the first occurrence of the pattern, the worst-case effi-ciency of the Boyer-Moore algorithm is known to be linear. Though this algorithm runs very fast, especially on large alphabets (relative to the length of the pattern), many people prefer its simplified versions, such as HorspoolŌĆÖs algorithm, when dealing with natural-languageŌĆōlike strings.
Exercises 7.2
1. Apply HorspoolŌĆÖs algorithm to search for the pattern BAOBAB in the text
BESS KNEW ABOUT BAOBABS
![]()
![]()
![]()
Consider the problem of searching for genes in DNA sequences using Hor-spoolŌĆÖs algorithm. A DNA sequence is represented by a text on the alphabet {A, C, G, T}, and the gene or gene segment is the pattern.
Construct the shift table for the following gene segment of your chromo-some 10:
TCCTATTCTT
Apply HorspoolŌĆÖs algorithm to locate the above pattern in the following DNA sequence:
TTATAGATCTCGTATTCTTTTATAGATCTCCTATTCTT
How many character comparisons will be made by HorspoolŌĆÖs algorithm in searching for each of the following patterns in the binary text of 1000 zeros?
a. 00001 b. 10000 c. 01010
For searching in a text of length n for a pattern of length m (n Ōēź m) with HorspoolŌĆÖs algorithm, give an example of
a. worst-case input. b. best-case input.
Is it possible for HorspoolŌĆÖs algorithm to make more character comparisons than the brute-force algorithm would make in searching for the same pattern in the same text?
If HorspoolŌĆÖs algorithm discovers a matching substring, how large a shift should it make to search for a next possible match?
How many character comparisons will the Boyer-Moore algorithm make in searching for each of the following patterns in the binary text of 1000 zeros?
a. 00001 b. 10000 c. 01010
a. Would the Boyer-Moore algorithm work correctly with just the bad-symbol table to guide pattern shifts?
Would the Boyer-Moore algorithm work correctly with just the good-suffix table to guide pattern shifts?
a. If the last characters of a pattern and its counterpart in the text do match, does HorspoolŌĆÖs algorithm have to check other characters right to left, or can it check them left to right too?
Answer the same question for the Boyer-Moore algorithm.
Implement HorspoolŌĆÖs algorithm, the Boyer-Moore algorithm, and the brute-force algorithm of Section 3.2 in the language of your choice and run an experiment to compare their efficiencies for matching
random binary patterns in random binary texts.
random natural-language patterns in natural-language texts.
You are given two strings S and T , each n characters long. You have to establish whether one of them is a right cyclic shift of the other. For example, PLEA is a right cyclic shift of LEAP, and vice versa. (Formally, T is a right cyclic shift of S if T can be obtained by concatenating the (n ŌłÆ i)-character suffix of S and the i-character prefix of S for some 1 Ōēż i Ōēż n.)
Design a space-efficient algorithm for the task. Indicate the space and time efficiencies of your algorithm.
Design a time-efficient algorithm for the task. Indicate the time and space efficiencies of your algorithm.
Related Topics