Definition, Formula, Solved Example Problems, Exercise | Mathematics - Input - output Analysis | 11th Business Mathematics and Statistics(EMS) : Chapter 1 : Matrices and Determinants
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 1 : Matrices and Determinants
Input - output Analysis
Input – output Analysis
Input –Output analysis is a technique which was invented by Prof. Wassily W.Leontief. Input Output analysis is a form of economic analysis based on the interdependencies between economic sectors. The method is most commonly used for estimating the impacts of positive or negative economic shocks and analyzing the ripple effects throughout an economy.
The foundation of Input - Output analysis involves input – output tables. Such tables include a series of rows and columns of data that quantify the supply chain for sectors of the economy. Industries are listed in the heads of each row and each column. The data in each column corresponds to the level of inputs used in that industry’s production function. For example the column for auto manufacturing shows the resources required for building automobiles (ie., requirement of steel, aluminum, plastic, electronic etc.,). Input – Output models typically includes separate tables showing the amount of labour required per rupee unit of investment or production.
Consider a simple economic model consisting of two industries A1 and A2 where each produces only one type of product. Assume that each industry consumes part of its own output and rest from the other industry for its operation. The industries are thus interdependent. Further assume that whatever is produced that is consumed. That is the total output of each industry must be such as to meet its own demand, the demand of the other industry and the external demand (final demand).
Our aim is to determine the output levels of each of the two industries in order to meet a change in final demand, based on knowledge of the current outputs of the two industries, of course under the assumption that the structure of the economy does not change.
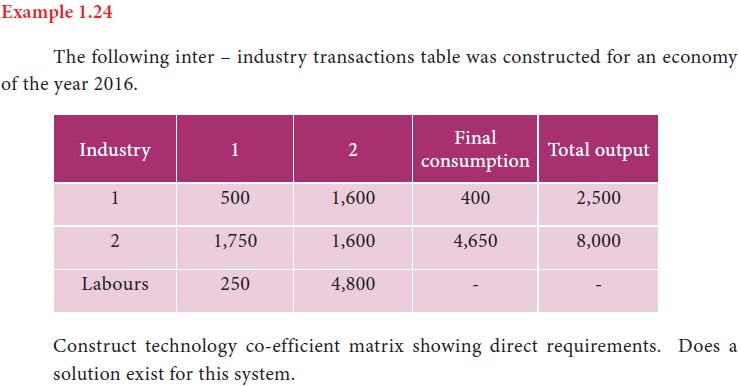
Let aij be the rupee value of the output of Ai consumed by Aj , i, j = 1, 2
Let x1 and x2 be the rupee value of the current outputs of A1 and A2 respectively.
Let d1 and d2 be the rupee value of the final demands for the outputs of A1 and A2 respectively.


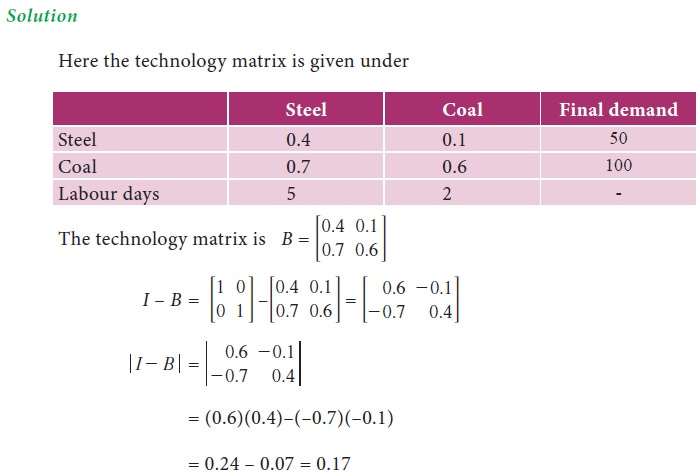
1. The Hawkins – Simon conditions
Hawkins – Simon conditions ensure the viability of the system.
If B is the technology matrix then Hawkins – Simon conditions are
i. the main diagonal elements in I – B must be positive and
ii. |I – B| must be positive.


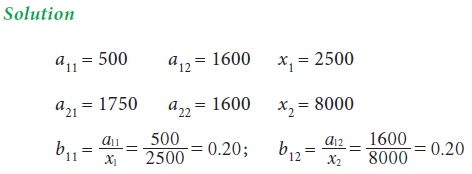



Example 1.26
An economy produces only coal and steel. These two commodities serve as intermediate inputs in each other’s production. 0.4 tonne of steel and 0.7 tonne of coal are needed to produce a tonne of steel. Similarly 0.1 tonne of steel and 0.6 tonne of coal are required to produce a tonne of coal. No capital inputs are needed. Do you think that the system is viable? 2 and 5 labour days are required to produce a tonne s of coal and steel respectively. If economy needs 100 tonnes of coal and 50 tonnes of steel, calculate the gross output of the two commodities and the total labour days required.



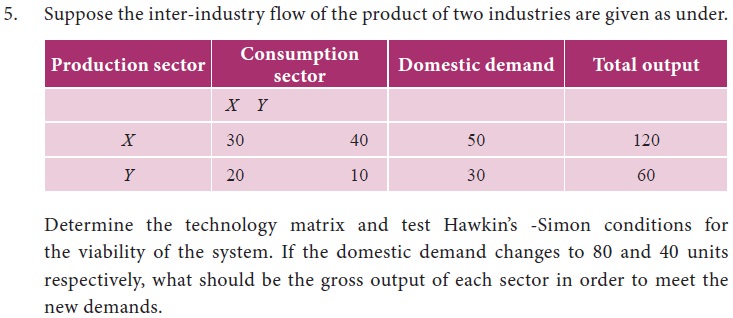
Related Topics