Determinants

Determinants

Introduction

The idea of a determinant was believed to be originated from a Japanese Mathematician Seki Kowa (1683) while systematizing the old Chinese method of solving simultaneous equations whose coefficients were represented by calculating bamboos or sticks. Later the German Mathematician Gottfried Wilhelm Von Leibnitz formally developed determinants. The present vertical notation was given in 1841 by Arthur Cayley. Determinant was invented independently by Crammer whose well known rule for solving simultaneous equations was published in 1750.

In class X, we have studied matrices and algebra of matrices. We have also learnt that a system of algebraic equations can be expressed in the form of matrices. We know that the area of a triangle with vertices (x₁, y₁) (x₂, y₂) and (x₃, y₃) is

To minimize the difficulty in remembering this type of expression, Mathematicians developed the idea of representing the expression in determinant form and the above expression can be represented in the form

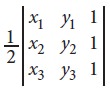
Thus a determinant is a particular type of expression written in a special concise form. Note that the quantities are arranged in the form of a square between two vertical lines. This arrangement is called a determinant.

In this chapter, we study determinants up to order three only with real entries. Also we shall study various properties of determinant (without proof), minors, cofactors, adjoint, inverse of a square matrix and business applications of determinants.

We have studied matrices in the previous class. Let us recall the basic concepts and operations on matrices.

1. Recall

Matrix

A matrix is a rectangular arrangement of numbers in horizontal lines (rows) and vertical lines (columns). Numbers are enclosed in square brackets or a open brackets or pair of double bars. It is denoted by A, B, C, …

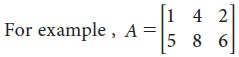
Order of a matrix

General form of a Matrix

Types of matrices

Row matrix

A matrix having only one row is called a row matrix.

Column matrix

A matrix having only one column is called a column matrix

Zero matrix (or) Null matrix

If all the elements of a matrix are zero, then it is called a zero matrix. It is represented by an English alphabet ‘O’

Square matrix

If the number of rows and number of columns of a matrix are equal then it is called a square matrix.

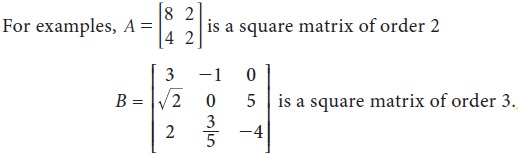
Triangular matrix

A square matrix, whose elements above or below the main diagonal (leading diagonal) are all zero is called a triangular matrix.

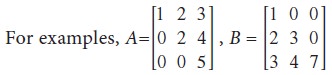
Diagonal matrix

A square matrix in which all the elements other than the main diagonal elements are zero is called the diagonal matrix.

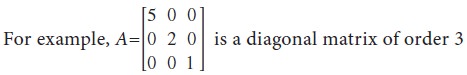
Scalar matrix

A diagonal matrix with all diagonal elements are equal to K (a scalar) is called a scalar matrix.

Unit matrix (or) Identity matrix

A scalar matrix having each diagonal element equal to one (unity) is called a Unit matrix.

Multiplication of a matrix by a scalar

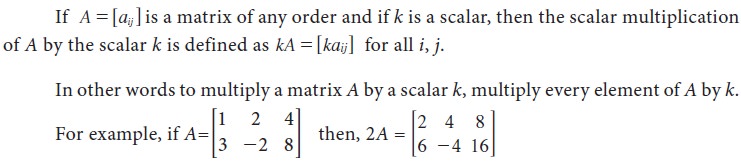
Negative of a matrix

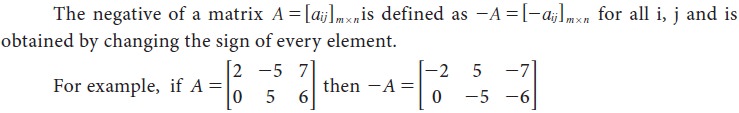
Equality of matrices

Two matrices A and B are said to be equal if

(i) they have the same order and  (ii) their corresponding elements are equal.

Addition and subtraction of matrices

Two matrices A and B can be added, provided both the matrices are of the same order. Their sum A+B is obtained by adding the corresponding entries of both the matrices

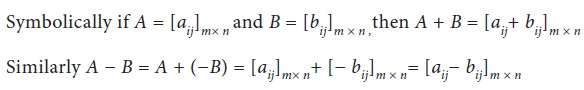
Multiplication of matrices

Multiplication of two matrices is possible only when the number of columns of the first matrix is equal to the number of rows of the second matrix. The product of matrices A and B is obtained by multiplying every row of matrix A with the corresponding elements of every column of matrix B element-wise and add the results.

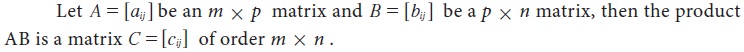
Transpose of a matrix

2. Minors:

Let | A | = |[a_ij]| be a determinant of order n. The minor of an arbitrary element a_ij is the determinant obtained by deleting the i^th row and j^th column in which the element a_ij stands. The minor of a_ij is denoted by M_ij.

3. Cofactors:

The cofactor is a signed minor. The cofactor of a_ij is denoted by A_ij and is defined as

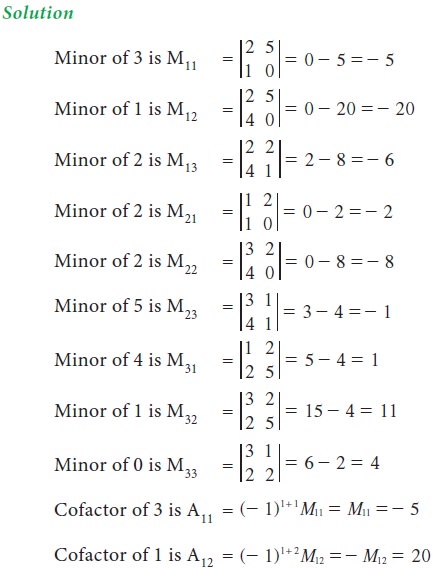
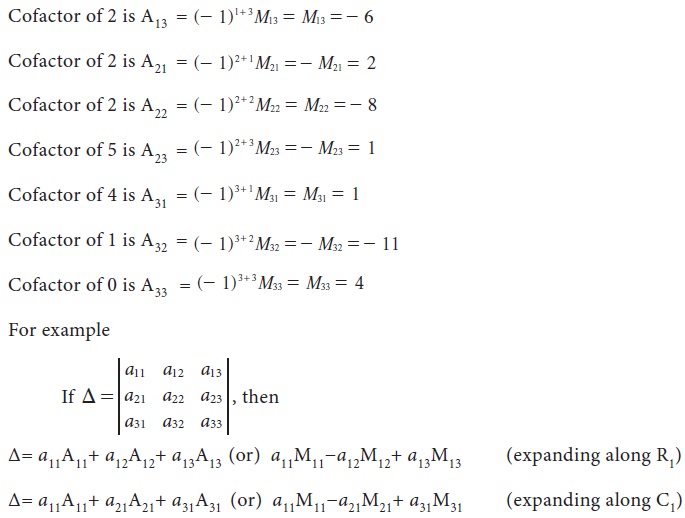
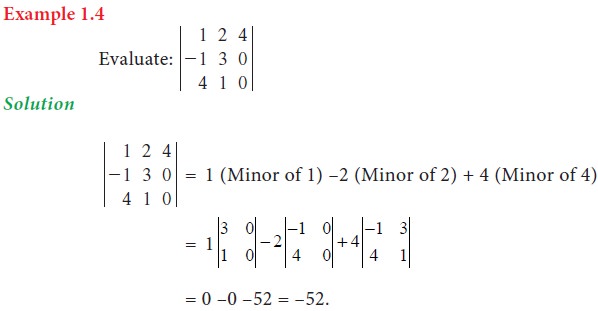
4. Properties of determinants (without proof)

1. The value of a determinant is unaltered when its rows and columns are interchanged

2. If any two rows (columns) of a determinant are interchanged then the value of the determinant changes only in sign.

3. If the determinant has two identical rows (columns) then the value of the determinant is zero.

4. If all the elements in a row (column) of a determinant are multiplied by constant k, then the value of the determinant is multiplied by k.

5. If any two rows (columns) of a determinant are proportional then the value of the determinant is zero.

6. If each element in a row (column) of a determinant is expressed as the sum of two or more terms, then the determinant can be expressed as the sum of two or more determinants of the same order.

7. The value of the determinant is unaltered when a constant multiple of the elements of any row (column) is added to the corresponding elements of a different row (column) in a determinant.