Important Questions and Answers: Properties of Surfaces and Solids

(PROPERTIES OF SURFACES AND SOLIDS)

1.     Define centroid of gravity.

Centroid is the geometrical center of the body whereas center of gravity is the point through which weight of the body acts.

2.  Difine first moment of an area about of an axis.

The first moment of an area about of an axis is the product of an area and the perpendicular distance of its centroid from axis.

3. Define line of symmetry.

Line of symmetry is line a about which the area on one side is a mirror image of the area of the side

4. State pappus-guldinus theorem for finding surface area.

The area of surface of revolution is equal to the product of the length of the generating curve and the distance travelled by the centroid of the generating curve while generating that surface.

5.What is uniform motion.

If the velocity of body does not change with time ,then the motion is called as uniform motion.

6.state parallel axis theorem.

Moment of inertia of an area about an axis is equal to the sum of (a) moment of inertia an axis passing through the centroid parallel to the given axis and (b) the product of area and square of the distance between the two parallel axes.

7.Define principal axes and principal moment of inertia.

The axes about which moments or inertia is maximum and minimum are known as principal axes .when these two axes are passing through centroid of aera it is known a centroidal principal axis.now the maximum and minimum moments of inertia are called principal moments of inertia.

8.What is called the coefficient of static friction.

As the force ‘P’ increases, ‘F’ also increases but the body remains at rest and is in equilibrium. If ‘F’ reaches a limiting value friction or from when ‘P’ is increases it loses its balance and hence the body slides to right.

9.state the Coulomb’s laws of dry friction.

(i)   when a body kept on another body is subjected to a horizontal force, friction force developed at the surfaces of contact of two bodies has a magnitude equal to that of the horizontal force applied. When one body moves over another,the magnitude of the friction force is less than that of the horizontal force.

(ii)   The friction force acts in the direction opposite to that of the moving body.

(iii)    The friction force is proportional to the normal reaction developed at the contact surface.

(iv)   The friction force does is not depend on the apparent area of the surfaces in contact

10.What is the condition in terms of efficiency for a machine to be self-locking.

When the efficiency of a machine is less than 50%, it is said to be self-locking

1. State parallel axis theorem 2.State perpendicular axis theorem

3.Find the polar moment of inertia of a hollow circular section of external diameter ‘D’ and internal diameter ‘d’

4.Define principal axes and principal moment of inertia

5.Locate the centroid and calculate the moment of inertia about centroidal axes of a semicircular lamina of radius 2m.

6.A semicircular area having a radius of 100 mm is located in the XY-plane such that its diameter

coincides with Y-axis.Determine the X-coordinate of the center. 7.Distiguish between centroid and center of gravity.

8.Define polar moment of inertia.

9.Differentiate between ‘Mass moment of inertia’ and ‘Area moment of inertia’

10.Write down the expression for finding mass moment of inertia of a cylinder of radius ‘R’ and height ‘h’ about its base.

1.       Determine the co-odinates of centroid of the shaded area shown in figure.

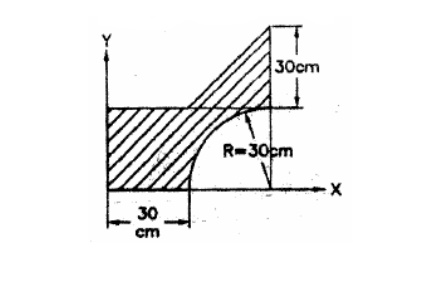
2. A Cylinder of height of 10 cm and radius of base 4 cm is placed under sphere of radius 4 cm such that they have a common vertical axis. If both of them are made of the same material, locate the centre of gravity of the combined unit.

3. Find the moment of inertia of the section shown in the figure about its horizontal centroidal axis.

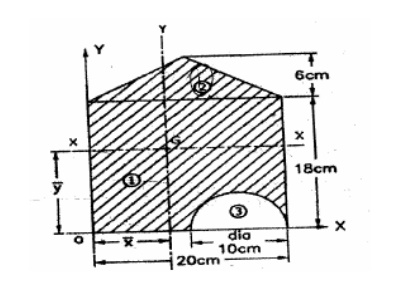
4. Calculate the mass moment of inertial of the plate shown in figure with respect to the axis AB. Thickness of the plate is 5 mm and density of the material is 6500 Kg/m3.

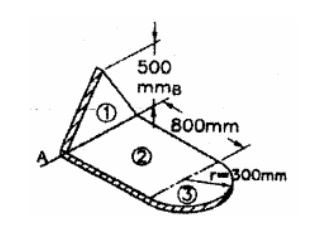
5. Derive expression form mass moment of inertia of prism along three axes.