Dynamics of Particles

DYNAMICS OF PARTICLES

1 Displacement

2 Angular Displacement

3 Angular Velocity

4 Angular Acceleration

5 Rectilinear motion

6 Curvilinear motion

7 Impulse and momentum

8 Newton’s law of motion

9 work energy Equation

1 Displacement

Change in position, that is, where an object is in relation to some reference point. It is measured in metres (m), and its symbol is usually, x, or s or sometimes d.

2 Angular Displacement

When an object moves along a straight path, we describe how far it has moved by its displacement. When an object rotates we describe how far it has rotated by its angular displacement .The mathematics of circular motion is much simpler if we measure the angle in radians rather than degrees. One radian as defined a s an angle whose arc length is equal to its radius, or in general:

3 Angular Velocity

The angular velocity is define d in relationship to the angular displacement in the same way that the linear velocity was defined in relationship to the linear displacement. The average angular velocity is given by the Greek le tter omega (w), and is defined as the rate of cha nge of the angular displacement.

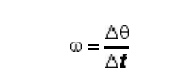
4 Angular Acceleration

Likewise, the average angula r acceleration is defined as the rate of change of the angular velocity, and is given by the Greek letter alpha.

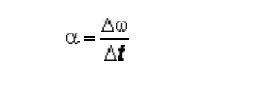
and the instantaneous angular ac celeration is given by;

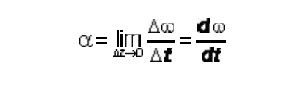
5 Rectilinear motion

The particle is classically re presented as a point placed somewhere in space . A rectilinear motion is a straight-line motion.

6 Curvilinear motion

The particle is classically represented as a point placed somewhere in space. A curvilinear motion is a motion along a curved path.

7 Impulse and momentum

Impulse

The impulse of the force is equal to the change of the momentum of the object.

Momentum

The total momentum bef ore the collision is equal to the total momentum after the collision

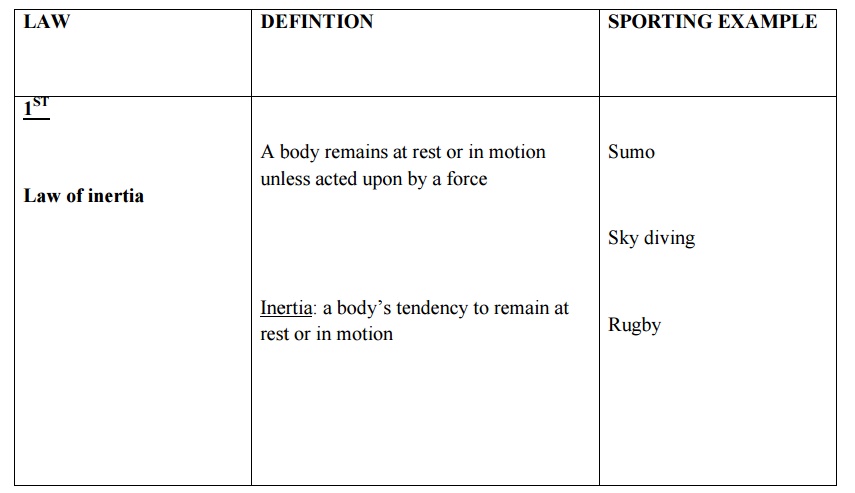
8 Newton’s law of motion

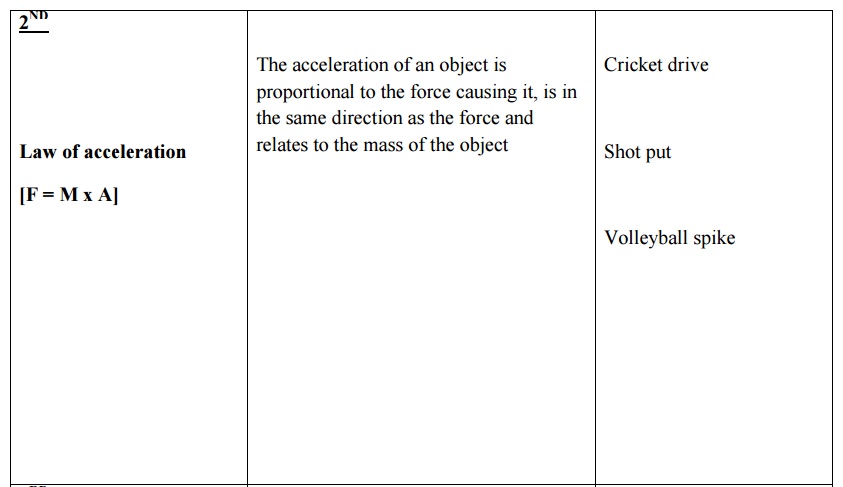
9 work energy Equvation

Energy in its different forms is a useful means of analysing Mechanics problems. The forms of energy include:

Kinetic Energy is the energy an object has due its motion.  It is calculated from the definition:

KE = ½ mv ².

The mass must be in kilograms, and the velocity in metres per second, and KE is measured in joules.Gravitational Potential Energy is the energy an object has due to its position, as with all forms of potential energy. In this case, the position is the position in a gravitational field, which can be measured from any reference point, but usually the surface of the earth. It is calculated from the definition:

Grav Pot’l E = mgh

The mass must be in kilograms, the value of ‘g’ is the acceleration due to gravity, 10 or 9.8 m/s², and ‘h’ is the height above the reference point. Again the unit of energy is joules.

Elastic Potential Energy is the energy stored in a compressed or stretched material.

Energy cannot be created or destroyed; it is just converted from one form to another. Other forms of energy include Light, Sound and Thermal energy. This means that the total amount of energy is constant or that Energy is conserved.