Hidden surface removal (HSR) and its algorithms

Hidden surface removal (HSR) and its algorithms

In 3D computer graphics, hidden surface determination (also known as hidden surface removal (HSR), occlusion culling (OC) or visible surface determination (VSD)) is the process used to determine which surfaces and parts of surfaces are not visible from a certain viewpoint. A hidden surface determination algorithm is a solution to the visibility problem, which was one of the first major problems in the field of 3D computer graphics. The process of hidden surface determination is sometimes called hiding, and such an algorithm is sometimes called a hider. The analogue for line rendering is hidden line removal. Hidden surface determination is necessary to render an image correctly, so that one cannot look through walls in virtual reality.

Hidden surface determination is a process by which surfaces which should not be visible to the user (for example, because they lie behind opaque objects such as walls) are prevented from being rendered. Despite advances in hardware capability there is still a need for advanced rendering algorithms. The responsibility of a rendering engine is to allow for large world spaces and as the world’s size approaches infinity the engine should not slow down but remain at constant speed. Optimising this process relies on being able to ensure the deployment of as few resources as possible towards the rendering of surfaces that will not end up being rendered to the user.

There are many techniques for hidden surface determination. They are fundamentally an exercise in sorting, and usually vary in the order in which the sort is performed and how the problem is subdivided. Sorting large quantities of graphics primitives is usually done by divide and conquer.

Hidden surface removal algorithms

Considering the rendering pipeline, the projection, the clipping, and the rasterization steps are handled differently by the following algorithms:

Z-buffering :

During rasterization the depth/Z value of each pixel (or sample in the case of anti-aliasing, but without loss of generality the term pixel is used) is checked against an existing depth value. If the current pixel is behind the pixel in the Z-buffer, the pixel is rejected, otherwise it is shaded and its depth value replaces the one in the Z-buffer. Z-buffering supports dynamic scenes easily, and is currently implemented efficiently in graphics hardware. This is the current standard. The cost of using Z-buffering is that it uses up to 4 bytes per pixel, and that the rasterization algorithm needs to check each rasterized sample against the z-buffer. The z-buffer can also suffer from artifacts due to precision errors (also known as z-fighting), although this is far less common now that commodity hardware supports 24-bit and higher precision buffers.

Coverage buffers (C-Buffer) and Surface buffer (S-Buffer):

faster than z-buffers and commonly used in games in the Quake I era. Instead of storing the Z value per pixel, they store list of already displayed segments per line of the screen. New polygons are then cut against already displayed segments that would hide them. An S-Buffer can display unsorted polygons, while a C-Buffer requires polygons to be displayed from the nearest to the furthest. Because the C-buffer technique does not require a pixel to be drawn more than once, the process is slightly faster. This was commonly used with BSP trees, which would provide sorting for the polygons.

Sorted Active Edge List

It is used in Quake 1, this was storing a list of the edges of already displayed polygons. Polygons are displayed from the nearest to the furthest. New polygons are clipped against already displayed polygons' edges, creating new polygons to display then storing the additional edges. It's much harder to implement than S/C/Z buffers, but it will scale much better with the increase in resolution.

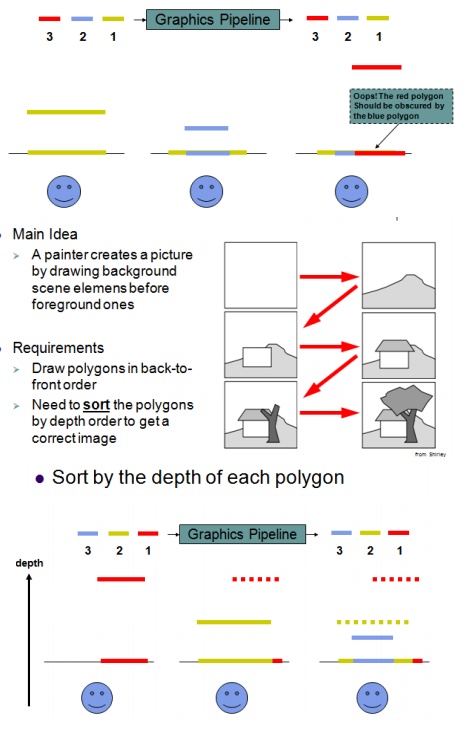
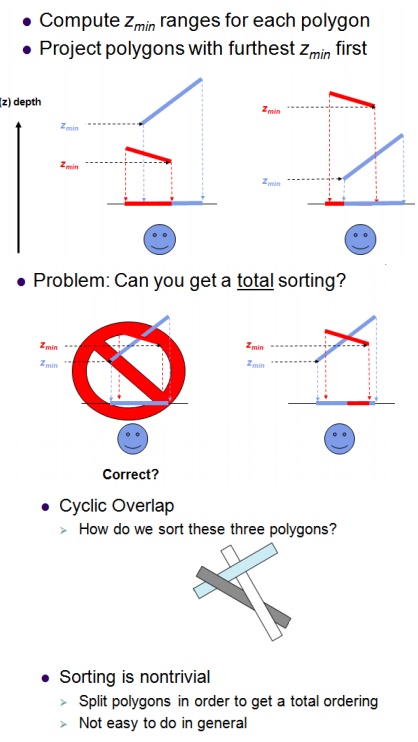
Painter's algorithm

It sorts polygons by their bary center and draws them back to front. This produces few artifacts when applied to scenes with polygons of similar size forming smooth meshes and back face culling turned on. The cost here is the sorting step and the fact that visual artifacts can occur.

Binary space partitioning (BSP)

It divides a scene along planes corresponding to polygon boundaries. The subdivision is constructed in such a way as to provide an unambiguous depth ordering from any point in the scene when the BSP tree is traversed. The disadvantage here is that the BSP tree is created with an expensive pre-process. This means that it is less suitable for scenes consisting of dynamic geometry. The advantage is that the data is pre-sorted and error free, ready for the previously mentioned algorithms. Note that the BSP is not a solution to HSR, only an aid.

Ray tracing

Attempt to model the path of light rays to a viewpoint by traci ng rays from the viewpoint into the scene . Although not a hidden surface removal algo rithm as such, it implicitly solves the hidd en surface removal problem by finding the nearest surface along each view-ray. Effectively this is equivalent to sorting all the geometry on a per pixel basis.

The Warnock algorithm

It divides the screen in to smaller areas and sorts triangles within t hese. If there is ambiguity (i.e., polygons ov erlap in depth extent within these areas), then f urther subdivision occurs. At the limit, subdivis ion may occur down to the pixel level.

Depth-Buffer Algorithm

•         Image-space method

•         Aka z-buffer algorithm

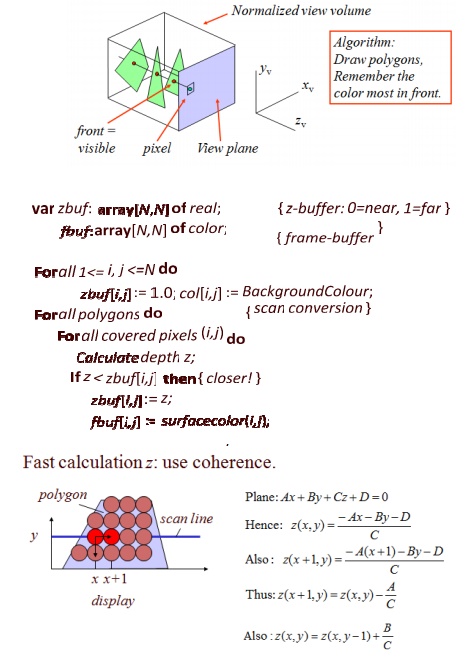
Advantages

Easy to implement

Hardware supported

Polygons can be processed in arbitrary order-

Fast: ~ #polygons, #covered pixels

Disadvantages

-       Costs memory

-       Color calculation sometimes done multiple times

-       Transparancy is tricky

Ray-casting Algorithm in hidden surface removal

•         Image-space method

•         Related to depth-buffer, order is different

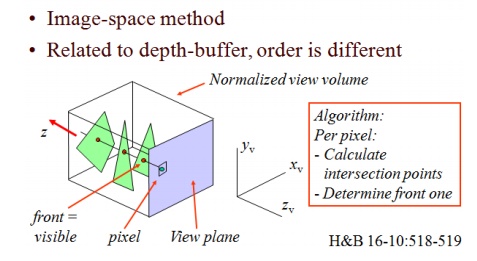
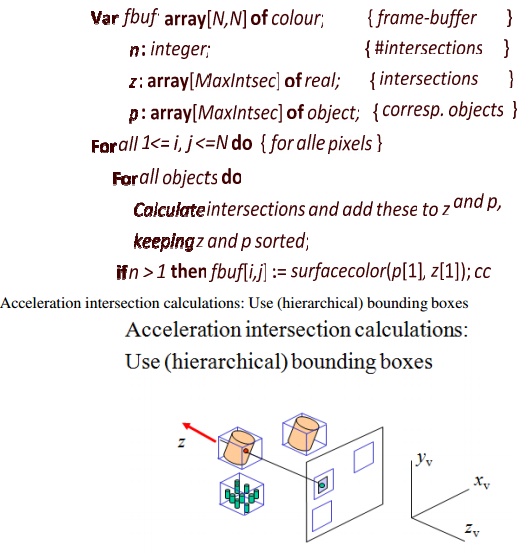
Advantages

+ Relatively easy to implement

+ For some objects very suitable (for instance spheres and other quadrati c surfaces)

+ Transparency can be de alt with easily

Disadvantages

-    Objects must be known in advance

-    Slow: ~ #objects*pixels, little coherence