Chapter: Transmission and Distribution : Insulators and Cables
Grading of Cables
GRADING OF CABLES
The process of achieving uniform electrostatic stress in the dielectric of cables is known as grading of cables.
It has already been shown that electrostatic stress in a single core cable has a maximum value (gmax) at the conductor surface and goes on decreasing as we move towards the sheath.
The maximum voltage that can be safely applied to a cable depends upon gmax i.e., electrostatic stress at the conductor surface. For safe working of a cable having homogeneous dielectric, the strength of dielectric must be more than gmax .If a dielectric of high strength is used for a cable, it is useful only near the conductor where stress is maximum. But as we move away from the conductor, the electrostatic stress decreases, so the dielectric will be unnecessarily over strong. The unequal stress distribution in a cable is undesirable for two reasons. Firstly, insulation of greater thickness is required which increases the cable size.
Secondly, it may lead to the break down of insulation. In order to overcome above disadvantages, it is necessary to have a uniform stress distribution in cables. This can be achieved by distributing the stress in such a way that its value is increased in the outer layers of dielectric. This is known as grading of cables. The following are the two main methods of grading of cables:
(i) Capacitance grading
(ii) Intersheath grading
(i)Capacitance Grading
The process of achieving uniformity in the dielectric stress by using layers of different dielectrics is known as capacitance grading.
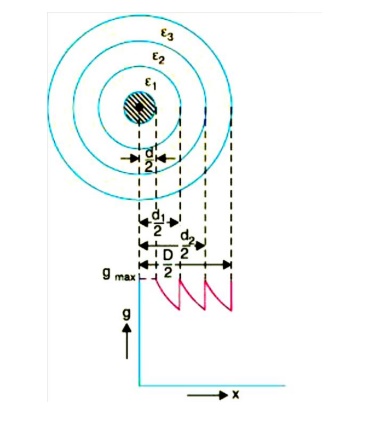
In capacitance grading, the homogeneous dielectric is replaced by a composite dielectric. The composite dielectric consists of various layers of different dielectrics in such a manner that relative permittivity r of any layer is inversely proportional to its distance from the center. Under such conditions, the value of potential gradient any point in the dielectric is constant and is independent of its distance from the center. In other words, the dielectric stress in the cable is same everywhere and the grading is ideal one. However, ideal grading requires the use of an infinite number of dielectrics which is an impossible task. In practice, two or three dielectrics are used in the decreasing order of permittivity, the dielectric of highest permittivity being used near the core. The capacitance grading can be explained beautifully by referring to Fig. There are three dielectrics of outer diameter d1, d2 and D and of relative permittivity 1, 2 and 3 respectively. If the permittivity are such that 1 > 2 > 3 and the three dielectrics are worked at the same maximum stress, then,


If the cable had homogeneous dielectric, then, for the same values of d, D and gmax, the permissible potential difference between core and earthed sheath would have been
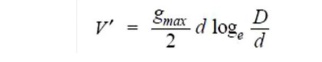
(ii)Intersheath Grading
In this method of cable grading, a homogeneous dielectric is used, but it is divided into various layers by placing metallic inters heaths between the core and lead sheath. The inter sheaths are held at suitable potentials which are in between the core potential and earth potential. This arrangement improves voltage distribution in the dielectric of the cable and consequently more uniform potential gradient is obtained.
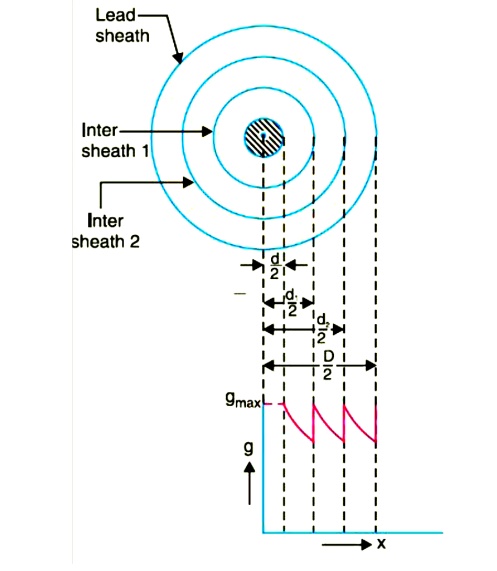
Consider a cable of core diameter d and outer lead sheath of diameter D. Suppose that two inters heaths of diameters d1 and d2 are inserted into the homogeneous dielectric and maintained at some fixed potentials. Let V1,V2 and V3 respectively be the voltage between core and intersheath 1, between inter sheath 1 and 2 and between inter sheath 2 and outer lead sheath. As there is a definite potential difference between the inner and outer layers of each inter sheath, therefore, each sheath can be treated like a homogeneous single core cable Maximum stress between core and inter sheath 1 is
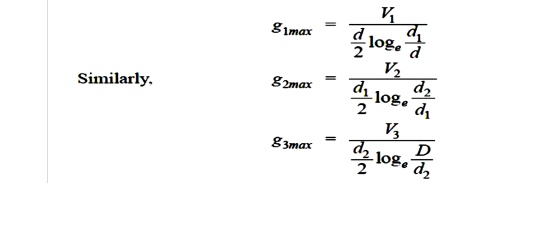
Since the dielectric is homogeneous, the maximum stress in each layer is the same i.e.,
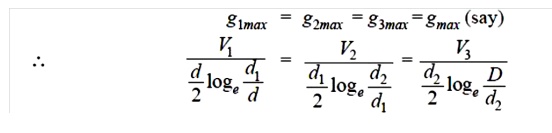
As the cable behaves like three capacitors in series, therefore, all the potentials are in phase i.e. Voltage between conductor and earthed lead sheath is
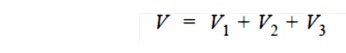
Inter sheath grading has three principal disadvantages. Firstly, there are complications in fixing the sheath potentials. Secondly, the inter sheaths are likely to be damaged during transportation and installation which might result in local concentrations of potential gradient. Thirdly, there are considerable losses in the inter sheaths due to charging currents. For these reasons, inter sheath grading is rarely used.
Capacitance of 3-core Cable
The capacitance of a cable system is much more important than that of overhead line because in cables
(i) conductors are nearer to each other and to the earthed sheath
(ii) they are separated bya dielectric of permittivity much greater than that of air.
Fig. shows a system of capacitances in a 3-core belted cable used for 3-phase system. Since potential difference exists between pairs of conductors and between each conductor and the sheath, electrostatic fields are set up in the cable as shown in Fig (i). These electrostatic fields give rise to core-core capacitances Cc and conductor-earth capacitances Ceas shown in Fig.(ii). The three Cc are delta connected whereas the three Ceare star connected, the sheath forming the star point
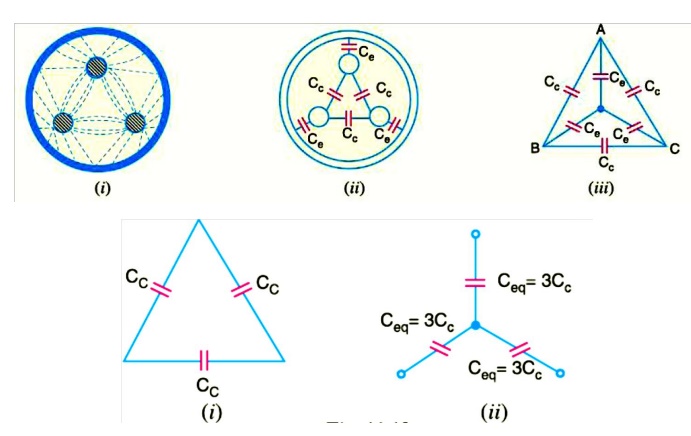

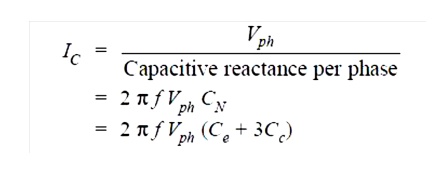
Related Topics