Chapter: Fundamentals of Database Systems : Database Design Theory and Normalization : Basics of Functional Dependencies and Normalization for Relational Databases
Functional Dependencies
Functional Dependencies
So far we have dealt with the informal measures of database design. We
now introduce a formal tool for analysis of relational schemas that enables us
to detect and describe some of the above-mentioned problems in precise terms.
The single most important concept in relational schema design theory is that of
a functional dependency. In this section we formally define the concept, and in
Section 15.3 we see how it can be used to define normal forms for relation
schemas.
Definition of
Functional Dependency
A functional dependency is a constraint between two sets of attributes from the database. Suppose that our relational database schema has n attributes A1, A2, ..., An; let us think of the whole database as being described by a single universal relation schema R = {A1, A2, ... , An}.7 We do not imply that we will actually store the database as a single universal table; we use this concept only in developing the for-mal theory of data dependencies.
Definition. A functional dependency, denoted by X → Y, between
two sets of attributes X and Y that are subsets of R
specifies a constraint on the
possible tuples that can form a relation state r of R. The constraint is
that, for any two tuples t1
and t2 in r that have t1[X] = t2[X], they must also have t1[Y] = t2[Y].
This
means that the values of the Y
component of a tuple in r depend on,
or are determined by, the values of
the X component; alternatively, the
values of the X com-ponent of a tuple
uniquely (or functionally) determine the values of the Y compo-nent. We also say that there is
a functional dependency from X to Y, or that Y is functionally dependent on X.
The abbreviation for functional dependency is FD or f.d. The set of
attributes X is called the left-hand side of the FD, and Y is called the right-hand side.
Thus, X functionally determines Y in a relation schema R if, and only if, whenever two tuples
of r(R) agree on their X-value,
they must necessarily agree on their Y-value.
Note the following:
If a constraint on R states that there cannot be more than one tuple with a given X-value in any relation instance r(R)—that
is, X is a candidate key of R—this
implies that X → Y for any
subset of attributes Y of R (because the key constraint implies that no two tuples in any legal state r(R)
will have the same value of X). If X is a candidate key of R, then X → R.
If X → Y in R, this does not say
whether or not Y → X in R.
A
functional dependency is a property of the semantics
or meaning of the attributes. The
database designers will use their understanding of the semantics of the attributes of R—that is, how they relate to one another—to specify the functional
dependencies that should hold on all
relation states (extensions) r of R. Whenever the semantics of two sets of
attributes in R indicate that a
functional dependency should hold, we specify the dependency as a constraint.
Relation extensions r(R) that satisfy the functional
dependency constraints are called legal
relation states (or legal extensions)
of R. Hence, the main use of functional dependencies is to describe further a relation schema R by specifying constraints on its
attributes that must hold at all times.
Certain FDs can be specified without referring to a specific relation, but as a
property of those attributes given their commonly understood meaning. For
example, {State, Driver_license_number} → Ssn should hold for any adult in the United States and hence should hold
whenever these attributes appear in a relation. It is also possible that
certain functional dependencies may cease to exist in the real world if the
relationship changes. For example, the FD Zip_code → Area_code used to exist as a relationship between postal
codes and telephone number codes in the United States, but with the
proliferation of telephone area codes it is no longer true.
Consider
the relation schema EMP_PROJ in
Figure 15.3(b); from the semantics of the attributes and the relation, we know
that the following functional dependencies should hold:
a. Ssn → Ename
b. Pnumber →{Pname, Plocation}
c. {Ssn, Pnumber} → Hours
These
functional dependencies specify that (a) the value of an employee’s Social
Security number (Ssn)
uniquely determines the employee name (Ename), (b)
the value of a project’s number (Pnumber)
uniquely determines the project name (Pname) and
location (Plocation), and
(c) a combination of Ssn and Pnumber values uniquely determines the
number of hours the employee currently works on the project per week (Hours). Alternatively, we say that Ename is functionally determined by
(or functionally dependent on) Ssn, or given a value of Ssn, we know the value of
Ename, and so on.
A
functional dependency is a property of
the relation schema R, not of a particular legal relation state r of R.
Therefore, an FD cannot be inferred
automatically from a given relation extension r but must be defined explicitly by someone who knows the semantics
of the attributes of R. For example,
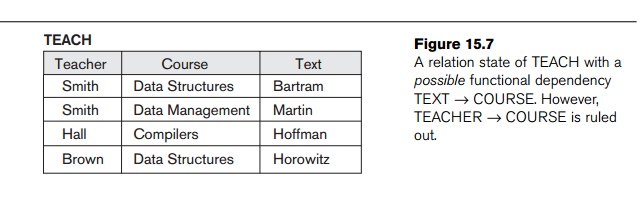
Figure 15.7 shows a particular state of the TEACH relation
schema. Although at first glance we may think that Text → Course, we cannot confirm this unless
we know that it is true for all possible legal states of TEACH. It is,
however, sufficient to demonstrate a
single counterexample to disprove
a functional dependency. For example, because ‘Smith’ teaches both ‘Data Structures’
and ‘Data Management,’ we can conclude that Teacher does not function-ally determine Course.
Given a
populated relation, one cannot determine which FDs hold and which do not unless
the meaning of and the relationships among the attributes are known. All one
can say is that a certain FD may
exist if it holds in that particular extension. One cannot guarantee its
existence until the meaning of the corresponding attributes is clearly
understood. One can, however, emphatically state that a certain FD does not
hold if there are tuples that show the
violation of such an FD. See the illustrative example relation in Figure 15.8. Here, the following FDs may hold because the four tuples in the
current extension have no violation of these constraints: B → C; C
→ B; {A, B}
→ C; {A, B}
→ D; and {C, D}
→ B. However,
the following do not hold because we
already have violations of them in the given extension: A → B (tuples 1 and 2 violate this
constraint); B → A (tuples 2 and 3 violate this con-straint); D → C (tuples 3 and 4 violate it).
Figure
15.3 introduces a diagrammatic notation
for displaying FDs: Each FD is dis-played as a horizontal line. The
left-hand-side attributes of the FD are connected by vertical lines to the line
representing the FD, while the right-hand-side attributes are connected by the
lines with arrows pointing toward the attributes.
We denote
by F the set of functional
dependencies that are specified on relation schema R. Typically, the schema designer specifies the functional
dependencies that are semantically
obvious; usually, however, numerous other functional dependencies hold in all legal relation instances among sets
of attributes that can be derived from and satisfy the dependencies in F. Those other dependencies can be inferred or deduced from the FDs in F.
We defer the details of inference rules and properties of functional dependencies to Chapter 16.
Related Topics