Boyce-Codd Normal Form

Boyce-Codd Normal Form

Boyce-Codd normal form (BCNF) was proposed as a simpler form of 3NF, but it was found to be stricter than 3NF. That is, every relation in BCNF is also in 3NF; however, a relation in 3NF is not necessarily in BCNF. Intuitively, we can see the need for a stronger normal form than 3NF by going back to the LOTS relation schema in Figure 15.12(a) with its four functional dependencies FD1 through FD4. Suppose that we have thousands of lots in the relation but the lots are from only two coun-ties: DeKalb and Fulton. Suppose also that lot sizes in DeKalb County are only 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0 acres, whereas lot sizes in Fulton County are restricted to 1.1, 1.2, ..., 1.9, and 2.0 acres. In such a situation we would have the additional func-tional dependency FD5: Area → County_name. If we add this to the other dependen-cies, the relation schema LOTS1A still is in 3NF because County_name is a prime attribute.

The area of a lot that determines the county, as specified by FD5, can be represented by 16 tuples in a separate relation R(Area, County_name), since there are only 16 pos-sible Area values (see Figure 15.13). This representation reduces the redundancy of repeating the same information in the thousands of LOTS1A tuples. BCNF is a stronger normal form that would disallow LOTS1A and suggest the need for decom-posing it.

Definition. A relation schema R is in BCNF if whenever a nontrivial functional dependency X → A holds in R, then X is a superkey of R.

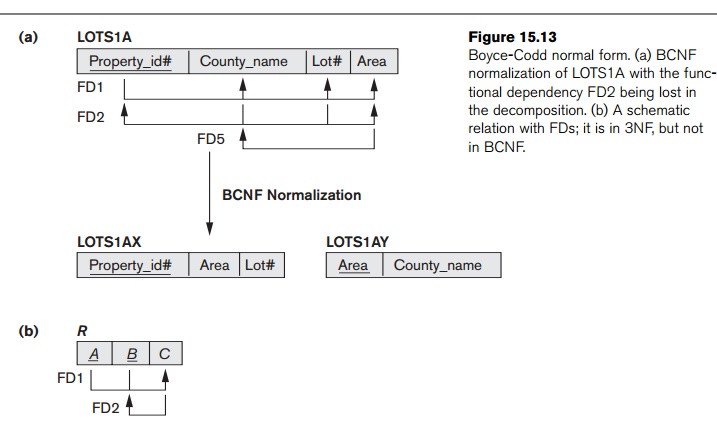
The formal definition of BCNF differs from the definition of 3NF in that condition (b) of 3NF, which allows A to be prime, is absent from BCNF. That makes BCNF a stronger normal form compared to 3NF. In our example, FD5 violates BCNF in LOTS1A because AREA is not a superkey of LOTS1A. Note that FD5 satisfies 3NF in LOTS1A because County_name is a prime attribute (condition b), but this condition does not exist in the definition of BCNF. We can decompose LOTS1A into two BCNF relations LOTS1AX and LOTS1AY, shown in Figure 15.13(a). This decomposition loses the functional dependency FD2 because its attributes no longer coexist in the same relation after decomposition.

In practice, most relation schemas that are in 3NF are also in BCNF. Only if X → A holds in a relation schema R with X not being a superkey and A being a prime attribute will R be in 3NF but not in BCNF. The relation schema R shown in Figure 15.13(b) illustrates the general case of such a relation. Ideally, relational database design should strive to achieve BCNF or 3NF for every relation schema. Achieving the normalization status of just 1NF or 2NF is not considered adequate, since they were developed historically as stepping stones to 3NF and BCNF.

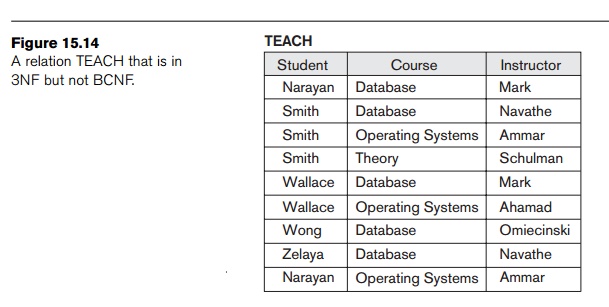
As another example, consider Figure 15.14, which shows a relation TEACH with the following dependencies:

FD1:                             {Student, Course} → Instructor

FD2:¹²                           Instructor → Course

Note that {Student, Course} is a candidate key for this relation and that the depen-dencies shown follow the pattern in Figure 15.13(b), with Student as A, Course as B, and Instructor as C. Hence this relation is in 3NF but not BCNF. Decomposition of this relation schema into two schemas is not straightforward because it may be

decomposed into one of the three following possible pairs:

        {Student, Instructor} and {Student, Course}.

        {Course, Instructor} and {Course, Student}.

        {Instructor, Course} and {Instructor, Student}.

All three decompositions lose the functional dependency FD1. The desirable decom-position of those just shown is 3 because it will not generate spurious tuples after a join.

A test to determine whether a decomposition is nonadditive (or lossless) is dis-cussed in Section 16.2.4 under Property NJB. In general, a relation not in BCNF should be decomposed so as to meet this property.

We make sure that we meet this property, because nonadditive decomposition is a must during normalization. We may have to possibly forgo the preservation of all functional dependencies in the decomposed relations, as is the case in this example. Algorithm 16.5 does that and could be used above to give decomposition 3 for TEACH, which yields two relations in BCNF as:

(Instructor, Course) and (Instructor, Student)

Note that if we designate (Student, Instructor) as a primary key of the relation TEACH, the FD Instructor → Course causes a partial (non-full-functional) depend-ency of Course on a part of this key. This FD may be removed as a part of second normalization yielding exactly the same two relations in the result. This is an example of a case where we may reach the same ultimate BCNF design via alternate paths of normalization.