Problem Questions with Answer, Solution | Mathematics - Exercise 2.1: Euclid’s Division Algorithm | 10th Mathematics : UNIT 2 : Numbers and Sequences
Chapter: 10th Mathematics : UNIT 2 : Numbers and Sequences
Exercise 2.1: Euclid’s Division Algorithm
Exercise 2.1
1. Find all positive integers, when divided by 3 leaves remainder 2.

2. A man has 532 flower pots. He wants to arrange them in rows such that each row contains 21 flower pots. Find the number of completed rows and how many flower pots are left over.

3. Prove that the product of two consecutive positive integers is divisible by 2.
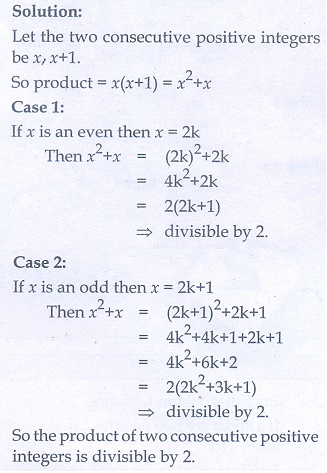
4. When the positive integers a , b and c are divided by 13, the respective remainders are9,7 and 10. Show that a+b+c is divisible by 13

5. Prove that square of any integer leaves the remainder either 0 or 1 when divided by 4.

6. Use Euclid’s Division Algorithm to find the Highest Common Factor (HCF) of
(i) 340 and 412
(ii) 867 and 255
(iii) 10224 and 9648
(iv) 84, 90 and 120

7. Find the largest number which divides 1230 and 1926 leaving remainder 12 in each case.

8. If d is the Highest Common Factor of 32 and 60, find x and y satisfying d = 32x + 60 y .

9. A positive integer when divided by 88 gives the remainder 61. What will be the remainder when the same number is divided by 11?

10. Prove that two consecutive positive integers are always coprime.

Answers:
1. 2, 5, 8, 11, …
2. 25, 7
6.(i) 4 (ii) 51 (iii) 144 (iv) 6
7. 174
8. 2 ,-1
9. 6
Related Topics