Evaluating arithmetic expressions

Evaluating arithmetic expressions

An example that demonstrated how to evaluate simple arithmetic expression such as 34 * 12. Now we are going to extend this problem to that of evaluating more complex arithmetic expressions. Initially, we are going to see how to handle expressions like

20 - 3 * 6 + 2

Eventually we will extend the basic algorithm to also handle parentheses, making it possible to evaluate expressions like

4 * ( 6 - 2 * (4 - 2))

Tokens

Because we are going to have to deal with inputs made up of many parts that have to be processed in an algorithm, the first step is to transform our input into a collection of objects that we can manipulate. If our input comes to us in the form of a String and the elements of the input are properly separated by spaces, we can start by using the String class's split() method to split the input String into an array of Strings.

This solves the problem of separating the input into individual elements we can manipulate. We are also going to go one step further, turning each of these elements into an object called a Token.

Tokens come in three basic types: numbers, operators, and parentheses. Tokens of type number have an associated numeric value, while operators will have an associated precedence value.

The TokenStack class

The basic algorithm for handling arithmetic expressions without parentheses makes use of a data structure called a stack. A stack is a container for a collection of data items. The data items are organized as a stack, with the first item to enter the container at the bottom and the last item at the top. When new items are added to the stack they are pushed onto the top of the stack. Items can only be removed from the stack by popping them off the top of the stack. For this algorithm the objects we are working with are Token objects, so we will need to construct a stack that can hold Tokens.

The basic algorithm

We are now ready to see the basic algorithm for computing arithmetic statements without parentheses. The algorithm makes use of two Token Stacks, a value stack and an operator stack. The basic algorithm processes the tokens from the input in a simple left to right order. Any number tokens that we encounter get pushed onto the value stack. When we encounter an operator token, we will push it onto the operator stack. At various points in the algorithm we will process an operator. We do this by popping the operator off of the operator stack and popping two numbers off the value stack. We then apply the operator to the two numbers to produce a result, package the result into a number token, and then push the number token back onto the top of the value stack. After the processing is complete, we discard the operator token. The most important logic in the evaluation algorithm tells us when to process the operators sitting on the operator stack. This logic is driven in part by the precedence of the operators involved: the operators + and - have a precedence of 1, while the operators * and / have a precedence of 2. Here are the key elements of the evaluation algorithm.

• If we encounter an operator token in the input and the operator stack is empty, we push the

operator token onto the operator stack.

• If we encounter an operator token in the input with a precedence that is greater than the precedence of the operator token at the top of the operator stack, we push the new operator token onto the operator stack.

• If we encounter an operator token in the input with a precedence that is less than or equal to the precedence of the operator token at the top of the operator stack, we process and remove the

operator at the top of the stack and then push the new operator token onto the operator stack.

• When we reach the end of the input, any operators that remain on the operator stack are processed and removed until the operator stack is empty. At that point, there should be only one number token left on the value stack: that number is the result of the evaluation.

An example

Here is an illustration of this algorithm in action. The expression we want to compute is 2 + 3 * 4 - 6

At the start of the algorithm both stacks are empty and the tokens are lined up in the input.

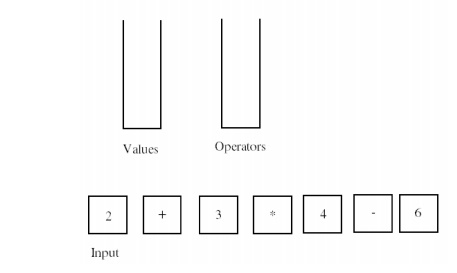
After handling the first three tokens we arrive at this configuration. 

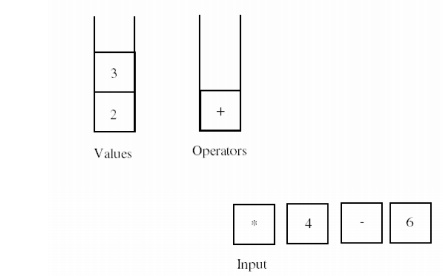
The next operator in the input has a higher precedence than the operator at the top of the operator stack, so we push the next operator. The next number token also gets pushed on the value stack.

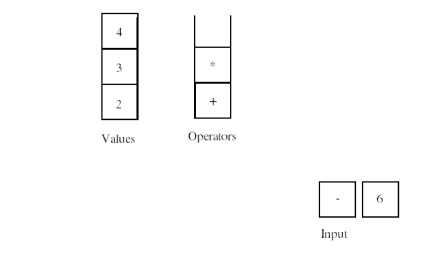
The next operator in the input sequence has a precedence lower than that of the operator at the top of the operator stack. This causes us to process and remove the operator at the top of the operator stack.

Once

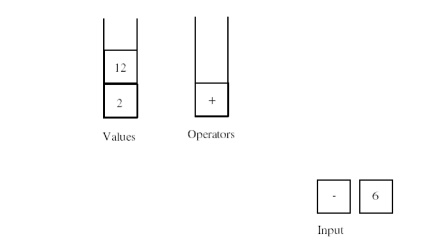
Once again, the operator in the input has a precendence equal to that of the operator at the top of the operator stack, so we process and remove the operator from the operator stack.

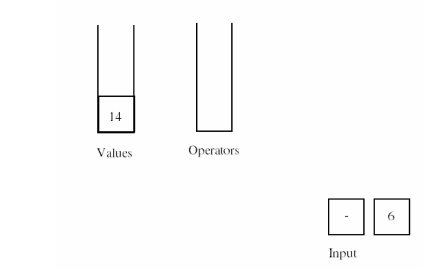
At this point the operator stack is empty, so the operator token at the front of the input gets pushed on the operator stack. The number token at the end of the input gets pushed on the value stack.

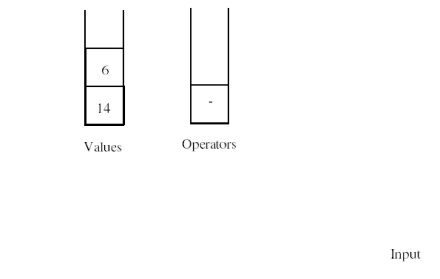
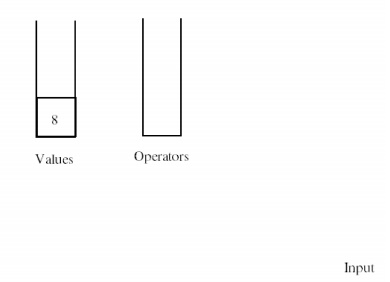
Once the input has emptied out, we process any operators that remain on the operator stack. Once all of those operators have been processed, the sole remaining number on the value stack is the result of the computation.

Handling parentheses

The algorithm outlined above can easily be extended to also handle parentheses correctly. All that is required is a couple of additional rules.

• When we encounter a left parentheses token in the input, we push that token on the operator stack.

• When we encounter a right parenthesis token in the input, we process operator s and remove them from the top of the operator stack until a left parenthesis appears at the top of the operator stack. We then pop off the left parenthesis token and discard both of the parenthesis tokens.