Enlargement and reduction of maps

Enlargement and reduction of maps

In the process of compiling maps cartographers are often required to either reduce or enlarge maps. Reduction or enlargement involves change in the size.

An enlargement provides the same map but proportionally larger than the original.

A reduction gives the same map that is proportionally smaller than the original.

The above image or map has been reduced by ½ .The amount that an original image has been enlarged or reduced is called a scale factor, or an enlargement or reduction factor. It is the constant factor by which all dimensions of an object are enlarged or reduced in a map. If shapes have been reduced by half, the scale factor is ½.

The ratio between the area of a map on one scale and its area to another scale is equal to the square of the ratios between the scales of the original and enlarged or reduced maps.

Graphical Method

Graphically maps can be enlarged or reduced with the help of similar squares.

The square method is the most common and simplest method for enlargement and reduction of maps. In order to enlarge a map, cover the original map with a set of squares of equal sides. The side of the squares has to be enlarged proportionally to that the original map.  The side of the square of the new map has to be determined using the formula.

Scale of the new map = New scale/old scale x Side of the square of the original map.

Example:

This is a map of Rajasthan drawn on a scale of 1/16,000,000 and is to be enlarged on the scale of 1/8,000,000.

To enlarge the given map on the scale of 1/8,000,000:

Step 1: Draw a network of squares on the original map, each side being 1 cm. in length.

Step 2: Calculation

When the scale is 1/16,000,000 the side of the small square is one cm.

For Scale of the map 1/16,000,000 side of the small square 51 cm

Therefore, If scale is to be 1/8,000,000 side of the small square of new map = x

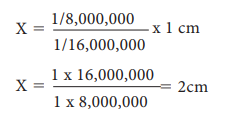
When the scale is 1/8,000,000 the side of the small square will be 2cmNow draw a network of squares, each side measuring 2 cm. The number of squares will be the same as on the original map. Now transfer the outline of original map on the enlarged map square by square.

Example :

This is a map of Madhya Pradesh drawn on a scale of 1/8,000,000 and is to be reduced on the scale of 1/16,000,000.

To reduce the given map on the scale of 1/16,000,000.

Step 1: Draw a network of squares on the original map, each side being 1 cm. in length.

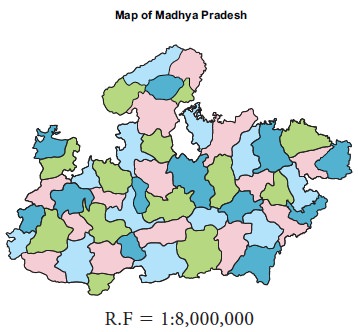
Step 2: Calculation

When the scale is 1/8,000,000, the side of the small square is one cm.

For Scale of the map 1/8,000,000, side of the small square 51 cm

Therefore, If scale is to be 1/16,000,000 side of the small square = x

When the scale is 1/16,000,000, the side of the small square will be ½ cm

Now draw a network of squares each side measuring 1/2 cm. of equal number

as on the original map and transfer its outline on the reduced map square by square.

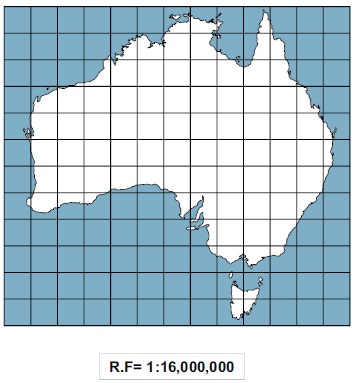
Example:

This is a map of Australia drawn on the scale of 1/32,000,000 and is to be enlarged on the scale of 1/16,000,000. The side of each square is ½ cm.

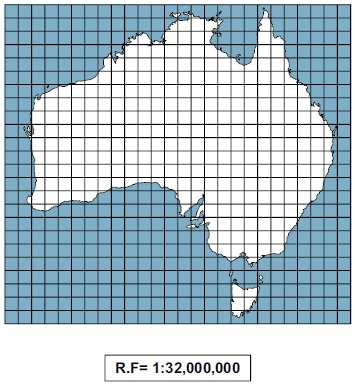
Calculation

To enlarged the given map on the scale of 1/16,000,000:

In the given map, when the scale is 1/32,000,000 the side of the small square is ½ cm.

Therefore, If scale is to be 1/16,000,000 side of the small square = x

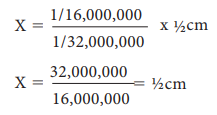
When the scale is 1/16,000,000 the side of the small square will be 1 cm. Now draw a network of squares, each side measuring 1 cm. The number of squares will be the same as on the original map. Now transfer the outline of original map on the enlarged map.

Exercise:

Trace the outline of any two districts of Tamil Nadu from your atlas and enlarge and reduce the same.