Probability | Maths - Empirical Approach | 9th Maths : UNIT 9 : Probability
Chapter: 9th Maths : UNIT 9 : Probability
Empirical Approach
Empirical Approach
For example, A manufacturer produces 10,000 electric switches every month and1,000
of them are found to be defective.
What is the probability of the manufacturer producing a defective switch every month?
The required
probability, according to relative frequency concept, is nearly 1000 out of 10000,
which is 0.1
Let us formalize
the definition: “If, the total number of trials, say n, we find r of the
outcomes in an event E, then the probability of event E, denoted by
P(E), is given by
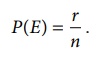
Note
The number of trials has to be large to decide this probability.
The larger the number of trials, the better will be the estimate of probability.
Is there
a guarantee that this value will settle down to a constant value when the number
of trials gets larger and larger? One cannot say; the concept being experimental,
it is quite possible to get distinct relative frequency each time the experiment
is repeated.
However,
there is a security range: the value of probability can at the least take the value
0 and at the most take the value 1. We can state this mathematically as
0≤
P(E)≤1.
Let us look
at this in a little detail.
First, we
know that r cannot be larger than n.
This means
r/n < 1. That is P(E) < 1 . … (1)
Next, if
r = 0, it means either the event cannot happen or has not occurred in a large
number of trials. (Can you get a 7, when you roll a dice?).
Thus , in
this case r/n = 0/n = 0 . … (2)
Lastly, if
r = n, the event must occur (in every trial or in a large number of
trials).
In such a
situation, r/n = n/n = 1 . … (3)
(getting
any number from 1 to 6 when you roll a dice)
From (1),
(2) and (3) we find 0 ≤ P (E) ≤
1.
Thinking Corner
For a question on probability the student’s answer was 3/2. The teacher
told that the answer was wrong. Why?
Progress Check
A random experiment was conducted. Which of these cannot be considered
as a probability of an outcome?
(i) 1/5 (ii) − 1/7 (iii) 0.40 (iv) − 0.52 (v) 0 (vi) 1.3 (vii) 1
(viii) 72% (ix) 107%
Example 9.1
When a dice
is rolled, find the probability to get the number which is greater than 4?
Solution
Sample space
S ={1,2,3,4,5,6}
Let E
be the event of getting a number greater than 4
={5,6}
P(E) = Number of favourable outcomes
/ Total number of outcomes
P(E) = n(E) /
n(S) = 2/6 = 0.333...
Example 9.2
In an office,
where 42 staff members work, 7 staff members use cars, 20 staff members use two-wheelers
and the remaining 15 staff members use cycles. Find the relative frequencies.
Solution
Total number
of staff members = 42.
The relative
frequencies:

In this example note that the total probability does not exceed 1
that is,
1/6 + 10/21 + 5/14 = 7/42 + 20/42 + 15/42 =1
Example 9.3
Team I and
Team II play 10 cricket matches each of 20 overs. Their total scores in each match
are tabulated in the table as follows:

What is the
relative frequency of Team I winning?
Solution
In this experiment,
each trial is a match where Team I faces Team II.
We are concerned
about the winning status of Team I.
There are
10 trials in total; out of which Team I wins in the 1st, 6th and 9th matches.
The relative
frequency of Team I winning the matches = 3/10 or 0.3.
(Note : The relative frequency depends on the sequence of outcomes that
we observe during the course of the experiment).
Related Topics