Electrical Circuits

DC Circuits:

A DC circuit (Direct Current circuit) is an electrical circuit that consists of any combination of constant voltage sources, constant current sources, and resistors. In this case, the circuit voltages and currents are constant, i.e., independent of time. More technically, a DC circuit has no memory. That is, a particular circuit voltage or current does not depend on the past value of any circuit voltage or current. This implies that the system of equations that represent a DC circuit do not involve integrals or derivatives.

If a capacitor and/or inductor is added to a DC circuit, the resulting circuit is not, strictly speaking, a DC circuit. However, most such circuits have a DC solution. This solution gives the circuit voltages and currents when the circuit is in DC steady state. More technically, such a circuit is represented by a system of differential equations. The solution to these equations usually contain a time varying or transient part as well as constant or steady state part. It is this steady state part that is the DC solution. There are some circuits that do not have a DC solution. Two simple examples are a constant current source connected to a capacitor and a constant voltage source connected to an inductor.

In electronics, it is common to refer to a circuit that is powered by a DC voltage source such as a battery or the output of a DC power supply as a DC circuit even though what is meant is that the circuit is DC powered.

Electric Current:

Electric current means, depending on the context, a flow of electric charge (a phenomenon) or the rate of flow of electric charge (a quantity). This flowing electric charge is typically carried by moving electrons, in a conductor such as wire; in an electrolyte, it is instead carried by ions, and, in a plasma, by both. The SI unit for measuring the rate of flow of electric charge is the ampere, which is charge flowing through some surface at the rate of one coulomb per second. Electric current is measured using an ammeter.

Current:

The flow of charge is called the current and it is the rate at which electric charges pass though a conductor. The charged particle can be either positive or negative. In order for a charge to flow, it needs a push (a force) and it is supplied by voltage, or potential difference. The charge flows from high potential energy to low potential energy. 

Current = I = Q / t

Where the symbol I to represent the quantity current.

Electro-magnetic force(E.M.F):

Electromotive Force is, the voltage produced by an electric battery or generator in an electrical circuit or, more precisely, the energy supplied by a source of electric power in driving a unit charge around the circuit. The unit is the volt. A difference in charge between two points in a material can be created by an external energy source such as a battery. This causes electrons to move so that there is an excess of electrons at one point and a deficiency of electrons at a second point. This difference in charge is stored as electrical potential energy known as emf. It is the emf that causes a current to flow through a circuit.

Voltage:

Voltage is electric potential energy per unit charge, measured in joules per coulomb ( = volts). It is often referred to as "electric potential", which then must be distinguished from electric potential energy by noting that the "potential" is a "per-unit-charge" quantity. Like mechanical potential energy, the zero of potential can be chosen at any point, so the difference in voltage is the quantity which is physically meaningful. The difference in voltage measured when moving from point A to point B is equal to the work which would have to be done, per unit charge, against the electric field to move the charge from A to B.

Electric potential:

A gravitational analogy was relied upon to explain the reasoning behind the relationship between location and potential energy. Moving a positive test charge against the direction of within Earth's gravitational field. Both movements would be like going against nature and would require work by an external force. This work would in turn increase the potential energy of the object. On the other hand, the movement of a positive test charge in the direction of an electric field would be like a mass falling downward within Earth's gravitational field. Both movements would be like going with nature and would occur without the need of work by an external force. This motion would result in the loss of potential energy. Potential energy is the stored energy of position of an object and it is related to the location of the object within a field.

Potential Difference:

A quantity related to the amount of energy needed to move an object from one place to another against various types of forces. The term is most often used as an abbreviation of "electrical potential difference", but it also occurs in many other branches of physics. Only changes in potential or potential energy (not the absolute values) can be measured.

Electrical potential difference is the voltage between two points, or the voltage drop transversely over an impedance (from one extremity to another). It is related to the energy needed to move a unit of electrical charge from one point to the other against the electrostatic field that is present. The unit of electrical potential difference is the volt (joule per coulomb). Gravitational potential difference between two points on Earth is related to the energy needed to move a unit mass from one point to the other against the Earth's gravitational field. The unit of gravitational potential differences is joules per kilogram.

Resistance:

Resistance is the ratio of potential difference across a conductor to the current flowing through it. If energy is used in passing electricity through an object, that object has a resistance.

Electromagnetism:

WhatisElectromagnetism?

When current passes through a conductor, magnetic field will be generated around the conductor and the conductor become a magnet. This phenomenon is called electromagnetism. Since the magnet is produced electric current, it is called the electromagnet. An electromagnet is a type of magnet in which the magnetic field is produced by a flow of electric current. The magnetic field disappears when the current ceases. In short, when current flow through a conductor, magnetic field will be generated.When the current ceases, the magnetic field disappear.

Applications of Electromagnetism:

Electromagnetism has numerous applications in today's world of science and physics. The very basic application of electromagnetism is in the use of motors. The motor has a switch that continuously switches the polarity of the outside of motor. An electromagnet does the same thing. We can change the direction by simply reversing the current. The inside of the motor has an electromagnet, but the current is controlled in such a way that the outside magnet repels it.

Another very useful application of electromagnetism is the "CAT scan machine." This machine is usually used in hospitals to diagnose a disease. As we know that current is present in our body and the stronger the current, the strong is the magnetic field. This scanning technology is able to pick up the magnetic fields, and it can be easily identified where there is a great amount of electrical activity inside the body.

The work of the human brain is based on electromagnetism. Electrical impulses cause the operations inside the brain and it has some magnetic field. When two magnetic fields cross each other inside the brain, interference occurs which is not healthy for the brain.

Ohm’s Law:

Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference or voltage across the two points, and inversely proportional to the resistance between them. The mathematical equation that describes this relationship is:

I= V/R

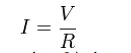
where I is the current through the resistance in units of amperes, V is the potential difference measured across the resistance in units of volts, and R is the resistance of the conductor in units of ohms. More specifically, Ohm's law states that the R in this relation is constant, independent of the current.

Resistance:

Resistance is the opposition that a substance offers to the flow of electric current. It is represented by the uppercase letter R. The standard unit of resistance is the ohm, sometimes written out as a word, and sometimes symbolized by the uppercase Greek letter omega. When an electric current of one ampere passes through a component across which a potential difference (voltage) of one volt exists, then the resistance of that component is one ohm.

In general, when the applied voltage is held constant, the current in a direct-current (DC) electrical circuit is inversely proportional to the resistance. If the resistance is doubled, the current is cut in half; if the resistance is halved, the current is doubled. This rule also holds true for most low-frequency alternating-current (AC) systems, such as household utility circuits.

In some AC circuits, especially at high frequencies, the situation is more complex, because some components in these systems can store and release energy, as well as dissipating or converting it.The electrical resistance per unit length, area, or volume of a substance is known as resistivity. Resistivity figures are often specified for copper and aluminum wire, in ohms per kilometre. Opposition to AC, but not to DC, is a property known as reactance. In an AC circuit, the resistance and reactance combine vectorially to yield impedance.

Voltage:

Introduction:

The voltage between two points is a short name for the electrical force that would drive an electric current between those points. Specifically, voltage is equal to energy per unit charge. In the case of static electric fields, the voltage between two points is equal to the electrical potential difference between those points. In the more general case with electric and magnetic fields that vary with time, the terms are no longer synonymous.

Electric potential is the energy required to move a unit electric charge to a particular place in a static electric field.Voltage can be measured by a voltmeter. The unit of measurement is the volt.

What is voltage?

Voltage should be more correctly called "potential difference". It is actually the electron moving force in electricity (emf) and the potential difference is responsible for the pushing and pulling of electrons or electric current through a circuit.

AC Circuits:

Fundamentals of AC:

An alternating current (AC) is an electrical current, where the magnitude of the current varies in a cyclical form, as opposed to direct current, where the polarity of the current stays constant.

The usual waveform of an AC circuit is generally that of a sine wave, as this results in the most efficient transmission of energy. However in certain applications different waveforms are used, such as triangular or square waves.

Used generically, AC refers to the form in which electricity is delivered to businesses and residences. However, audio and radio signals carried on electrical wire are also examples of alternating current. In these applications, an important goal is often the recovery of information encoded (or modulated) onto the AC signal.

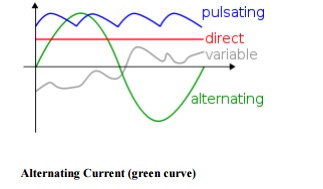
Alternating Current (green curve)

AC Instantaneous and RMS:

Instantaneous Value:

The INSTANTANEOUS value of an alternating voltage or current is the value of voltage or current at one particular instant. The value may be zero if the particular instant is the time in the cycle at which the polarity of the voltage is changing. It may also be the same as the peak value, if the selected instant is the time in the cycle at which the voltage or current stops increasing and starts decreasing. There are actually an infinite number of instantaneous values between zero and the peak value.

RMS Value:

The average value of an AC waveform is NOT the same value as that for a DC waveforms average value. This is because the AC waveform is constantly changing with time and the heating effect given by the formula ( P = I ².R ), will also be changing producing a positive power consumption. The equivalent average value for an alternating current system that provides the same power to the load as a DC equivalent circuit is called the "effective value". This effective power in an alternating current system is therefore equal to: ( I².R.Average ).

As power is proportional to current₂ Avesquared,. Therefore, the effective current in an AC system is called the Root Mean Squared or R.M.S.

RLC Series Circuit:

An RLC circuit (or LCR circuit) is an electrical circuit consisting of a resistor, an inductor, and a capacitor, connected in series. I is the current through the circuit.

V_R = IR, voltage drop across R

V_L = IX_L, voltage drop across L

V_C= IX_C, voltage drop across C

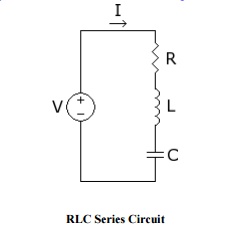
RLC Series Circuit

DIFFERENCE BETWEEN AC AND DC:

Current that flows continuously in one direction is called direct current. Alternating current (A.C) is the current that flows in one direction for a brief time then reverses and flows in opposite direction for a similar time. The source for alternating current is called a.c generator or alternator.

Cycle:

One complete set of positive and negative  values of an alternating quantity is called cycle.

Frequency:

The number of cycles made by an alternating quantity per second is called frequency. The unit of frequency is Hertz(Hz)

Amplitude or Peak value

The maximum positive or negative value of an alternating quantity is called amplitude or peak value.

Average value:

This is the average of instantaneous values of an alternating quantity over one complete cycle of the wave.

Time period:

The time taken to complete one complete cycle. Average value derivation:

Let i = the instantaneous value of current And i = Im sin ɵ

Where,  Im is the maximum value.

Kirchholaw:ff’s

Kirchoff's Current Law:

First law (Current law or Point law):

The sum of the currents flowing towards any junction in an electric circuit equal to the sum of currents flowing away from the junction.

Kirchoff's Current law can be stated in words as the sum of all currents flowing into a node is zero. Or conversely, the sum of all currents leaving a node must be zero. As the image below demonstrates, the sum of currents Ib, Ic, and Id, must equal the total current in Ia. Current flows through wires much like water flows through pipes. If you have a definite amount of water entering a closed pipe system, the amount of water that enters the system must equal the amount of water that exists the system. The number of branching pipes does not change the net volume of water (or current in our case) in the system.

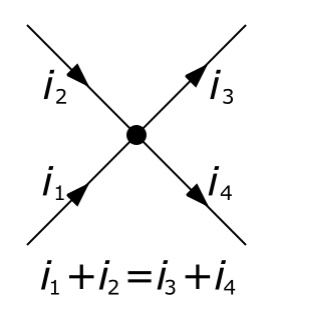
Kirchoff's Voltage Law:

Second law (voltage law or Mesh law):

In any closed circuit or mesh, the algebraic sum of all the electromotive forces and the voltage drops is equal to zero.

Kirchoff's voltage law can be stated in words as the sum of all voltage drops and rises in a closed loop equals zero. As the image below demonstrates, loop 1 and loop 2 are both closed loops within the circuit. The sum of all voltage drops and rises around loop 1 equals zero, and the sum of all voltage drops and rises in loop 2 must also equal zero. A closed loop can be defined as any path in which the originating point in the loop is also the ending point for the loop. No matter how the loopis defined or drawn, the sum of the voltages in the loop must be zero

Problems and Calculations:

Problem 1:

A current of 0.5 A is flowing through the r between its ends.

Solution:

Current I    = 0.5A.

Resistance R = 10Ω Potential difference V = ?

V   = IR

=   0.5 × 10 = 5V.

Problem :2

A supply voltage of 220V is applied to a flowing through it.

Solution:

Voltage V = 220V     

Resistance R     =       100Ω

Current I =       V/R  =         220/100 = 2.2 A.

Problem : 3

Calculate the resistance of the conductor if a current of 2A flows through it when the potential difference across its ends is 6V.

Solution:

Current I = 2A. Potential difference = V = 6. Resistance R = V/I

=   6 /2

=   3 ohm.

Problem: 4

Calculate the current and resistance of a 100 W ,200V electric bulb.

Solution:

Power,P  = 100W

Voltage,V = 200V

Power p = VI

Current I = P/V = 100/200  = 0.5A

Resistance R = V /I = 200/0.5  = 400W.

Problem: 5

Calculate the power rating of the heater coil when used on 220V supply taking 5 Amps.

Solution:

Voltage ,V = 220V

Current ,I = 5A, Power,P = VI = 220 × 5

= 1100W = 1.1 KW.

Problem: 6

A circuit is made of 0.4wire,Ωa 150Ω bulb and a 120Ω rheo connected in series. Determine the total resistance of the resistance of the circuit.

Solution:

Resistance of the wire = 0.4Ω Resistance of bulb = 150Ω Resistance of rheostat = 120Ω

In series,

Total resistance ,R = 0.4 + 150 +120 = 270.4Ω

Problem :7

In the circuit shown in fig .find the current, voltage drop across each resistor and the power dissipated in each resistor.

Solution:

Total resistance of the circuit = 2 + 6 +7 R = 15 Ω

Voltage ,V =   4 5V

Circuit current ,I =  V /R =   45 /15   =  3A

Voltage drop across 2Ω   resistor=IR₁   V₁

=  3 × 2 = 6 Volts.

Voltage drop across 6Ω resistor V₂ = I R₂

= 3 × 6  = 18 volts.

Voltage             drop   acrossV3=IR₃ = 7Ω   resistor

= 3 × 7 = 21 volts.

Power dissipated in R₁ is P₁      = P R₁

= 32 × 2 = 18 watts.

Power dissipated in R₂ is P₂     = I₂ R₂.

= 32 × 6 = 54 watts.

Power dissipated in R₃ is P₃   = I₂ R₃.

= 32 × 7 = 63 watts.

Problem : 8

Three resistances of values 2Ω,3Ω and 5Ω are co supply .Calculate (a) equivalent resistance of the circuit (b) the total current of the

circuit (c) the voltage drop across each resistor and (d) the power dissipated in each

resistor.

Solution:

Total resistance R = R₁ + R₂+ R₃.

= 2 +3+5 = 10Ω

Voltage           = 20V

Total current I   = V/R = 20/10 = 2A.

Voltage drop   acrossV1=IR1   2Ω   resistor

= 2× 2  = 4 volts.

Voltage drop   acrossV₂=IR2   3Ω   resistor

= 2 × 3 = 6 volts.

Voltage drop   acrossV₃=IR₃  5Ω   resistor

= 2 ×5 = 10 volts.

Power dissipated = in I₂R₁ 2Ω   resistor   is   P1

      = 22  × 2    = 8 watts.

Power dissipated in 3 resistor is P₂  = I₂ R₂.

      =       22 × 3         = 12 watts.

Power dissipated in 5 resistor is P₃ = I₂ R₃

      =       22      × 5    = 20 watts.

Problem: 9

A lamp can work on a 50 volt mains taking 2 amps.What value of the resistance must be connected in series with it so that it can be operated from 200 volt mains giving the same power.

Solution:

Lamp voltage ,V = 50V Current ,I = 2 amps.

Resistance of the lamp = V/I = 50/25 =   25   Ω

Resistance connected in series with lamp = r. Supply voltage = 200 volt.

Circuit current I = 2A

Total resistance Rt= V/I = 200/2 = 100Ω Rt = R + r

100 = 25 + r

r = 75Ω