Divide and Conquer Method

DIVIDE AND CONQUER

Divide and Conquer is one of the best-known general algorithm design technique. Divide-and-conquer algorithms work according to the following general plan:

1.A problem's instance is divided into several smaller instances of the same problem, ideally of about the same size.

2.  The smaller instances are solved (typically recursively, though sometimes a different algorithm is employed when instances become small enough).

3.  If necessary, the solutions obtained for the smaller instances are combined to get a solution to the original problem.

The divide-and-conquer technique is diagrammed, which depicts the case of dividing a problem into two smaller sub problems,

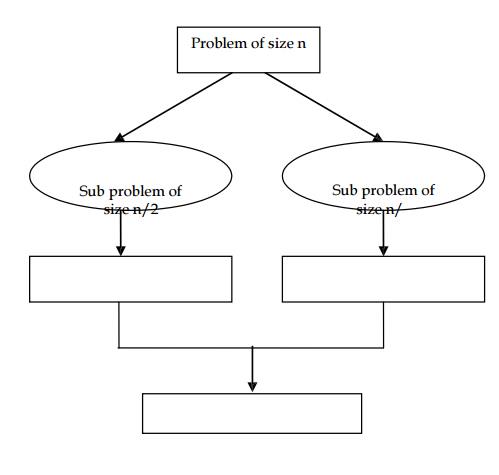
Examples of divide and conquer method are Binary search, Quick sort,

GENERAL METHOD

e.g. Merge sort.

♦ As an example, let us consider the problem of computing the sum of n numbers a₀, ... a_n-1.

♦  If n > 1, we can divide the problem into two instances of the same problem. They are To compute the sum of the first └ n/2┘numbers

♦  To compute the sum of the remaining [n/2]numbers. (Of course, if n = 1, we simply return a₀ as the answer.)

♦    Once  each  of  these  two  sums  is  computed  (by  applying  the  same  method,  i.e.,

recursively),

we can add their values to get the sum in question. i.e.,

a₀ + . . . + a_n-1 =( a₀  + ....+ a└ _n/2┘) + (a└ _n/2┘ + . . . . + a_n-1)

♦  More generally, an instance of size n can be divided into several instances of size nib, with a of them needing to be solved. (Here, a and b are constants; a≥1 and b > 1.).

♦  Assuming that size n is a power of b, to simplify our analysis, we get the following recurrence for the running time T(n).

T(n)=aT(n/b)+f(n)

♦ This is called the general divide and-conquer recurrence. Where f(n) is a function that accounts for the time spent on dividing the problem into smaller ones and on combining their solutions. (For the summation example, a = b = 2 and f (n) = 1.

♦ Obviously, the order of growth of its solution T(n) depends on the values of the constants a and b and the order of growth of the function f (n). The efficiency analysis of many divide-and-conquer algorithms is greatly simplified by the following theorem.

1. MASTER THEOREM

ADVANTAGES:

♦ The time spent on executing the problem using divide and conquer is smaller then other methods.

♦ The divide and conquer approach provides an efficient algorithm in computer science.

♦ The divide and conquer technique is ideally suited for parallel computation in which each sub problem can be solved simultaneously by its own processor.

♦  Merge sort is a perfect example of a successful application of the divide-and conquer technique.

♦  It sorts a given array Al O .. n - 1) by dividing it into two halves A [O··└ n/2┘ - 1] and A[└

n/2┘..n - 1], sorting each of them recursively, and then merging the two smaller sorted arrays into a single sorted one.

ALGORITHM Mergesort (A[O .. n - 1])

//Sorts array A[O .. n - 1] by recursive mergesort //Input: An array A[O .. n - 1] of orderable elements //Output: Array A[O... n - 1] sorted in nondecreasing order if n > 1

copy A [O··└ n/2┘ - 1] to B [O··└ n/2┘ - 1] copy A[└ n/2┘..n - 1] to C[0...└ n/2┘ - 1] Mergesort (B [O··└ n/2┘ - 1])

Mergesort (C[0...└ n/2┘ - 1]) Mergesort(B,C,A)

STEPS TO BE FOLLOWED

♦ The first step of the merge sort is to chop the list into two.

♦ If the list has even length, split the list into two equal sub lists.

♦  If the list has odd length, divide the list into two by making the first sub list one entry greater than the second sub list.

♦ then split both the sub list into two and go on until each of the sub lists are of size one.

♦ finally, start merging the individual sub lists to obtain a sorted list.

♦ The operation of the algorithm for the array of elements 8,3,2,9,7,1,5,4 is explained as follows,

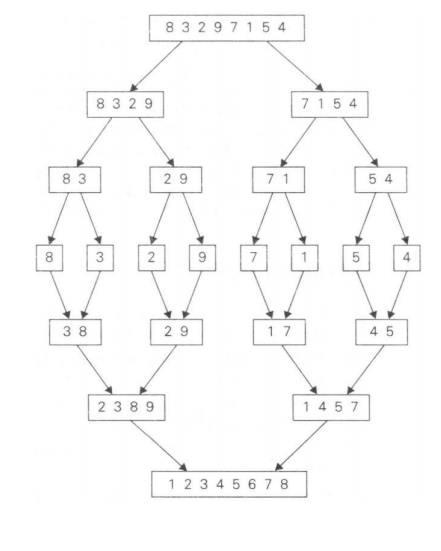
AN EXAMPLE OF MERGE SORT OPEERATION

♦  The merging of two sorted arrays can be done as follows. Two pointers (array indices) are initialized to point to the first elements of the arrays being merged.

♦  Then the elements pointed to are compared and the smaller of them is added to a new array or list being constructed.

♦   Then the index of the smaller element is incremented to point to its immediate successor in the array.

♦   This  operation  is  continued  until  one  of  the  two  given  arrays  is  exhausted

♦Then         the remaining elements of the other  array  are copied to the end of the new

array.                  

          ALGORITHM : Merge Sort B(0....p-1), C(0....    q-1), A(0....p + q -1)

// Merges two sorted arrays into one sorted array .

// Input: Array B (0....p-1) and C (0....q-1) both sorted

//Output: Sorted array A (0....p + q -1) of the elements of B and C

i ^f 0; j ^f0 ;k^f 0 while i<p and j<q do if B[i] ≤ C[j]

A[k] ^fB[i];i ^fi+1

else A[k] ^f C[j] j^f j+1 k ^fk+1

if i=p

copy C[j....q-1] to A[k....p+q-1] else copy B[i....p-1] to A[k....p+q-1]

2 EFFICIENCY OF MERGE SORT

♦ The recurrence relation for the number of key comparison C (n) is

C (n) = 2 C (n/2) + C_merge (n) for n>1, C (1) = 0

♦ Assume, n is a power of 2. C_merge (n) is the number of key comparison performed during the merge sort.

♦  In the merging of two sorted array after one comparison is made the total number of elements in the two array still to be processed and sorted is reduced by one.

♦  Hence in the worst case neither of the two arrays becomes empty before the other one contains just one element . Therefore, for the worst case,

C _worst(n)=2 C _worst(n / 2)+n-1 for n > 1, C _worst(1)=0

C_merge(n) = n – 1

and we have the recurrence

Hence, according to the Master Theorem, C worst (n)  = (n log n) . In fact, it is easy to find the exact solution to the worst-case recurrence for n = 2k

C worst(n) = n log2 n - n + 1