Binary Search Algorithm

BINARY SEARCH

♦   The binary search algorithm is one of the most efficient searching techniques which require the list to be sorted in ascending order.

♦  To search for an element in the list, the binary search algorithms split the list and locate the middle element of the list.

♦ The middle of the list is calculated as

Middle:=(l+r) div 2

n – number of element in list

♦ The algorithm works by comparing a search key element ‗k‘ with the array middle element a[m]

After comparison, any one of the following three conditions occur.

1.     If the search key element 'k‘ is greater than a[m],then the search element is only in the upper or second half and eliminate the element present in the lower half.Now the value of l is middle m+1.

2.     If the search key element 'k‘ is less than a[m], then the search element is only in the lower or first half. No need to check in the upper half. Now the value of r is middle m - 1.

3.     If the search key element 'k‘ is equal to a[m], then the search key element is found in the position m. Hence the search operation is complete.

EXAMPLE:

The list of element are 3,14,27,31,39,42,55,70,74,81,85,93,98 and searching for k=70 in the list.

m – middle element 

m = n div 2

=13 div 2 

m = 6

If k>a[m], then ,l =7. So, the search element is present in second half .

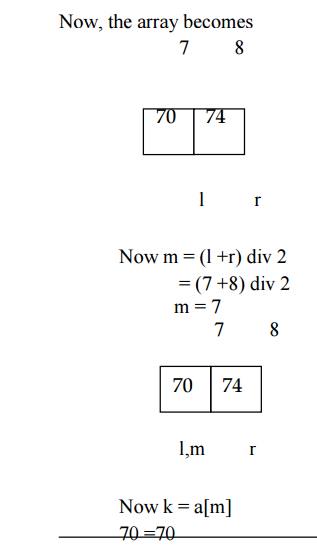
Hence, the search key element 70 is found in the position 7 and the search operation is completed.

ALGORITHM: Binary search (A[0..n – 1],k) //Implements nonrecursive binary search

//  Input:: An array A[0..n – 1] sorted in ascending order and a search key k

//  Output: An index of the array’s element that is equal to k or -1 if there is no

//                             such element

l^! 0; r ^! n – 1 while l<= r do

m ^! └(l + r)/ 2 ┘

if k = A[m] return m

else if k < A[m] r ^! m – 1 else l ^! m+ 1

return -1

 EFFICIENCY OF BINARY SEARCH

♦ The standard way to analyze the efficiency is to count number of times search key is compared with an element of the array.

WORST CASE ANALYSIS

♦ The worst case include all array that do not contain a search key.

♦ The recurrence relation for C_worst(n) is

= 1 + └log₂i┘ + 1 =2 +└ log₂i┘

C_worst(n ) =2 +└ log₂i┘

R.H.S becomes

C_worst└ n / 2 ┘+ 1= C_worst└2i /2┘ + 1 =C_worst(i) + 1

=     log₂i + 1 + 1

= 2 +└ log₂i┘

C_worst└ n  / 2┘ + 1 =2 +└ log₂i┘

L.H.S =R.H.S

Hence

C_worst(n ) = └log₂n ┘+ 1 and

C_worst(i ) = └log₂i ┘+ 1 are same

Hence

From equation (4) to search a element in a array of 1000 elements ,binary search takes. └ log₂10³ ┘ + 1 = 10 key comparison

AVERAGE CASE ANALYSIS:

Average number of key comparison made by the binary search is slightly smaller than worst case.

Cavg (n) ≈ log₂  n

The average number of comparison in the successful search is C^yes _avg (n) ≈ log₂ n – 1

The average number of comparison in the unsuccessful search is C^no _avg (n) ≈ log₂ (n + 1)

ADVANTAGES

1.     In this method elements are eliminated by half each time .So it is very faster than the sequential search.

2.     It requires less number of comparisons than sequential search to locate the search key element.

DISADVANTAGES

1.     An insertion and deletion of a record requires many records in the existing table be physically moved in order to maintain the records in sequential order.

2.     The ratio between insertion/deletion and search time is very high.