Container Loading Algorithm

CONTAINER LOADING

The greedy algorithm constructs the loading plan of a single container layer by layer from the bottom up. At the initial stage, the list of available surfaces contains only the initial surface of size L x W with its initial position at height 0. At each step, the algorithm picks the lowest usable surface and then determines the box type to be packed onto the surface, the number of the boxes and the rectangle area the boxes to be packed onto, by the procedure select layer.

The procedure select layer calculates a layer of boxes of the same type with the highest evaluation value. The procedure select layeruses breadth-limited tree search heuristic to determine the most promising layer, where the breadth is different depending on the different depth level in the tree search. The advantage is that the number of nodes expanded is polynomial to the maximal depth of the problem, instead of exponentially growing with regard to the problem size. After packing the specified number of boxes onto the surface according to the layer arrangement, the surface is divided into up to three sub-surfaces by the procedure divide surfaces.

Then, the original surface is deleted from the list of available surfaces and the newly generated sub-surfaces are inserted into the list. Then, the algorithm selects the new lowest usable surface and repeats the above procedures until no surface is available or all the boxes have been packed into the container. The algorithm follows a similar basic framework.

The pseudo-code of the greedy algorithm is given by the greedy heuristic procedure.

procedure greedy heuristic()

list of surface := initial surface of L x W at height 0 list of box type := all box types

while (there exist usable surfaces) and (not all boxes are packed) do

select the lowest usable surface as current surface set depth := 0

set best layer := select layer(list of surface, list of box type, depth)

pack best layer on current surface

reduce the number of the packed box type by the packed amount

set a list of new surfaces := divide surfaces(current surface, best layer, list of box type)

delete current surface from the list of surfaces

insert each surface in list of new surfaces into list of surfaces

end while

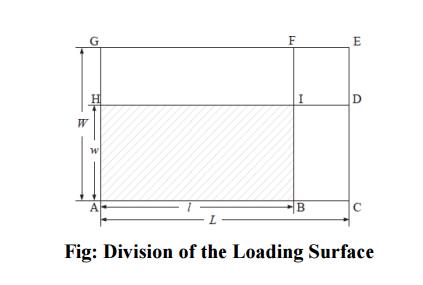
Given a layer of boxes of the same type arranged by the G4-heuristic, the layer is always packed in the bottom-left corner of the loading surface.

As illustrated in above Figure, up to three sub-surfaces are to be created from the original loading surface by the procedure divide surfaces, including the top surface, which is above the layer just packed, and the possible spaces that might be left at the sides.

If l = L or w = W, the original surface is simply divided into one or two sub-surfaces, the top surface and a possible side surface. Otherwise, two possible division variants exist, i.e., to divide into the top surface, the surface (B,C,E,F) and the surface (F,G,H, I), or to divide into the top surface, the surface (B,C,D, I) and the surface (D,E,G,H).

The divisions are done according to the following criteria, which are similar to those in [2] and [5]. The primary criterion is to minimize the total unusable area of the division variant. If none of the remaining boxes can be packed onto a sub-surface, the area of the sub-surface is unusable. The secondary criterion is to avoid the creation of long narrow strips.

―The underlying rationale is that narrow areas might be difficult to fill subsequently‖. More specifically, if L−l ≥ W −w, the loading surface is divided into the top surface, the surface (B,C,E,F) and the surface (F,G,H, I). Otherwise, it is divided into the top surface, the surface (B,C,D, I) and the surface (D,E,G,H).

Algorithm for Container Loading