Decomposition

Decomposition

Problem decomposition is one of the elementary problem-solving techniques. It involves breaking down a problem into smaller and more manageable problems, and combining the solutions of the smaller problems to solve the original problem. Often, problems have structure. We can exploit the structure of the problem and break it into smaller problems. Then, the smaller problems can be further broken until they become sufficiently small to be solved by other simpler means. Their solutions are then combined together to construct a solution to the original problem.

1. Refinement

After decomposing a problem into smaller subproblems, the next step is either to refine the subproblem or to abstract the subproblem.

1.           Each subproblem can be expanded into more detailed steps. Each step can be further expanded to still finer steps, and so on. This is known as refinement.

2.           We can also abstract the subproblem. We specify each subproblem by its input property and the input-output relation. While solving the main problem, we only need to know the specification of the subproblems. We do not need to know how the subproblems are solved.

Example 7.6. Consider a school goer's action in the morning. The action can be written as

1. Get ready for school

We can decompose this action into smaller, more manageable action steps which she takes in sequence:

1. Eat breakfast

2. Put on clothes

3. Leave home

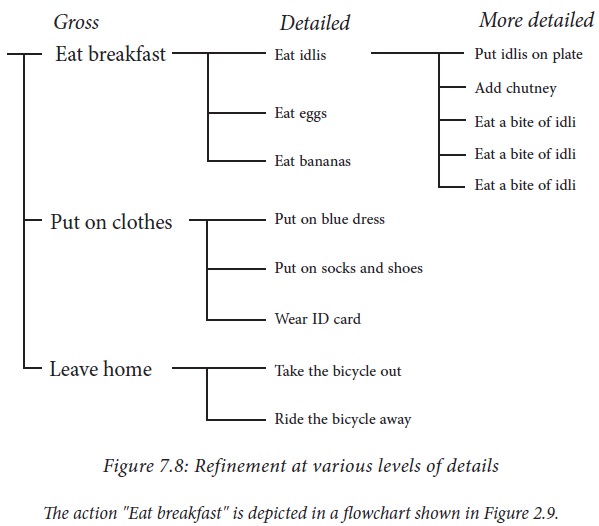
We have refined one action into a detailed sequence of actions. However, each of these actions can be expanded into a sequence of actions at a more detailed level, and this expansion can be repeated. The action "Eat breakfast" can be expanded as

1. -- Eat breakfast

2. Eat idlis

3. Eat eggs

4. Eat bananas

The action "Put on clothes" can be expanded as

1. -- Put on clothes

2. Put on blue dress

3. Put on socks and shoes

4  Wear ID card

and "Leave home" expanded as

1. -- Leave home

2. Take the bicycle out

3  Ride the bicycle away

Thus, the entire action of "Get ready for school" has been refined as

1-- Eat breakfast

2Eat idlis

3 Eat eggs

4. Eat bananas

5

6 -- Put on clothes

7      Put on blue dress

8 Put on socks and shoes

9  Wear ID card

10

11 -- Leave home

12 Take the bicycle out

13 Ride the bicycle away

Refinement is not always a sequence of actions. What the student does may depend upon the environment. How she eats breakfast depends upon how hungry she is and what is on the table; what clothes she puts on depends upon the day of the week. We can refine the behaviour which depends on environment, using conditional and iterative statements.

1 -- Eat breakfast

2 if hungry and idlis on the table

3 Eat idlis

4  if hungry and eggs on the table

5 Eat eggs

6  if hungry and bananas on the table

7    Eat bananas

8 -- Put on clothes

10 if Wednesday

11 Put on blue dress

12 else

13 Put on white dress

14 Put on socks and shoes

15 Wear the ID card

16

17 -- Leave home

18 Take the bicycle out

19 Ride the bicycle away

The action "Eat idlis" can be further refined as an iterative action:

1 -- Eat idlis

2 Put idlis on the plate

3 Add chutney

4 while idlis in plate

5 Eat a bite of idli

How "Get ready for school" is refined in successive levels is illustrated in Figure 7.8.

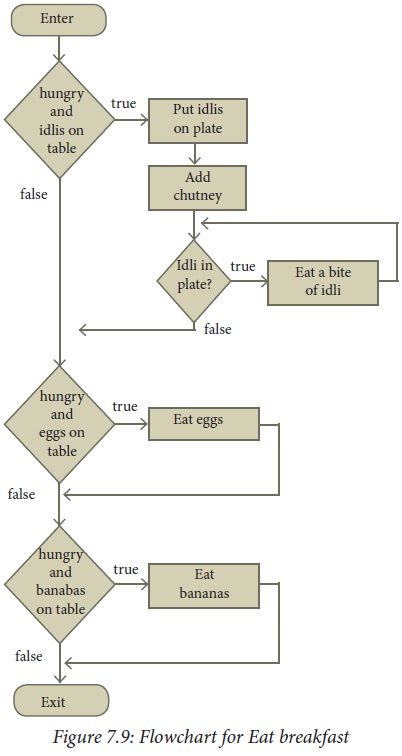
Note that the flowchart does not show the hierarchical structure of refinement.

2. Functions

After an algorithmic problem is decomposed into subproblems, we can abstract the subproblems as functions. A function is like a sub-algorithm. Similar to an algorithm, a function is specified by the input property, and the desired input-output relation.

To use a function in the main algorithm, the user need to know only the specification of the function — the function name, the input property, and the input-output relation. The user must ensure that the inputs passed to the function will satisfy the specified property and can assume that the outputs from the function satisfy the input-output relation. Thus, users of the function need only to know what the function does, and not how it is done by the function. The function can be used a a "black box" in solving other problems.

Ultimately, someone implements the function using an algorithm. However, users of the function need not know about the algorithm used to implement the function. It is hidden from the users. There is no need for the users to know how the function is implemented in order to use it.

An algorithm used to implement a function may maintain its own variables. These variables are local to the function in the sense that they are not visible to the user of the function. Consequently, the user has fewer variables to maintain in the main algorithm, reducing the clutter of the main algorithm.

Example 7.7. Consider the problem of testing whether a triangle is right-angled, given its three sides a, b, c, where c is the longest side. The triangle is right-angled, if

c² = a² + b²

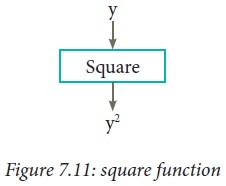
We can identify a subproblem of squaring a number. Suppose we have a function square(), specified as

square(y)

--inputs : y

--outputs : y2

we can use this function three times to test whether a triangle is right-angled. square() is a "black box" — we need not know how the function computes the square. We only need to know its specification.

1 right_angled(a, b, c)

2   -- inputs: c ≥ a, c ≥ b

3   -- outputs: result = true if c² = a² + b²;

4 -- result = false , otherwise

5 if square (c) = square (a) + square (b)

6 result := true

7   else

8 result := false