Computer Science - Composition | 11th Computer Science : Chapter 7 : Composition and Decomposition
Chapter: 11th Computer Science : Chapter 7 : Composition and Decomposition
Composition
Composition
A statement is a phrase that
commands the computer to do an action. We have already seen assignment
statement. It is a simple statement, used to change the values of variables.
Statements may be composed of other statements, leading to a hierarchical
structure of algorithms. Statements composed of other statements are known as
compound statements.
Control flow statements are
compound statements. They are used to alter the control flow of the process
depending on the state of the process. There are three important control flow
statements:
• Sequential
• Alternative
• Iterative
When a control flow statement is
executed, the state of the process is tested, and depending on the result, a
statement is selected for execution.
1. Sequential statement
A sequential statement is composed
of a sequence of statements. The statements in the sequence are executed one
after another, in the same order as they are written in the algorithm, and the
control flow is said to be sequential. Let S1 and S2 be statements. A
sequential statement composed of S1 and S2 is written as
o S1
o S2
In order to execute the sequential
statement, first do S1 and then do S2.
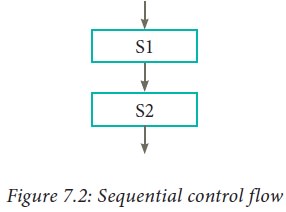
The sequential statement given
above can be represented in a flowchart as shown in in Figure 7.2. The arrow
from S1 to S2 indicates that S1 is executed, and after that, S2 is executed.
Let the input property be P, and
the input-output relation be Q, for a problem. If statement S solves the
problem, it is written as
-- P
S
-- Q
If we decompose the problem into
two components, we need to compose S as a sequence of two statements S1 and S2
such that the input-output relation of S1, say R, is the input property of S2.
• -- P
• S1
• -- R
• S2
• -- Q
Example 7.1. Let us solve the Farmer, Goat, Grass, and Wolf problem of Example 6.12. We decided to represent the state of the process by four variables farmer, goat, grass, and wolf, representing the sides of the farmer, goat, grass and wolf, respectively. In the initial state, all four variables have the value L (Left side). In the final state, all four variables should have the value R (Right side). The goal is to construct a statement S so as to move from the initial state to the final state.
1. -- farmer, goat,
grass, wolf = L, L, L,
L
2. S
3. -- farmer , goat , grass , wolf = R, R, R, R
We have to compose S as a sequence
of assignment statements such that in none of the intermediate states
1. goat and wolf have the same
value but farmer has the opposite value, or
2. goat and grass have the same
value but farmer has the opposite value.Subject to these constraints, a
sequence of assignments and the state after each assignment are shown in Figure
7.3.

Other than lines (1) and (15), in
line (7), goat and grass have the same value, but farmer also has the same
value as they. In line (9), goat and wolf have the same value, but farmer also
has the same value as they. Thus, the sequence has achieved the goal state,
without violating the constraints.
2. Alternative statement
S1 and S2 are statements, then
if C
S1
else
S2
is a statement, called an
alternative statement, that describes the following action:
1.
Test
whether C is true or false.
2.
If C
is true, then do S1; otherwise do S2.
In pseudo code, the two
alternatives S1 and S2 are indicated by indenting them from the keywords if and
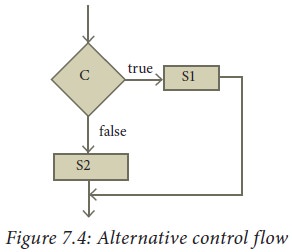
else, respectively. Alternative control flow is depicted in the flowchart of
Figure 2.4. Condition C has two outgoing arrows, labeled true and false. The
true arrow points to the S1 box. The false arrow points to the S2 box. Arrows
out of S1 and S2 point to the same box, the box after the alternative
statement.
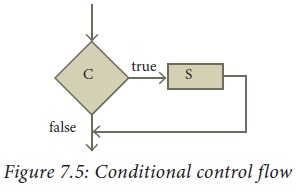
Conditional statement: Sometimes we need to execute a statement only
if a condition is true and do nothing if the condition is false. This is
equivalent to the alternative statement in which the else-clause is empty. This
variant of alternative statement is called a conditional statement. If C is a
condition and S is a statement, then
if C
S
is a statement, called a
conditional statement, that describes the following action:
1.
Test
whether C is true or false.
2.
If C
is true then do S; otherwise do nothing.
The conditional control flow is
depicted in the flowchart of Figure 2.5.
Example 7.2. Minimum of two numbers: Given two numbers a and b, we want
to find the minimum of the two using the alternative statement. Let us store
the minimum in a variable named result. Let a ↓ b denote the minimum of a and b
(for instance, 4 ↓ 2 = 2, —5 ↓ 6 = -5). Then, the specification of algorithm
minimum is
minimum(a, b)
--input s : a , b
--outputs: result = a ↓ b
Algorithm minimum can be defined
as
• minimum(a, b)
• -- a, b
• if a < b
• result : = a
• else
• result = b
• -- result = a ↓ b
3. Case analysis
Alternative statement analyses the
problem into two cases. Case analysis statement generalizes it to multiple
cases. Case analysis splits the problem into an exhaustive set of disjoint
cases. For each case, the problem is solved independently. If C1, C2, and C3
are conditions, and S1, S2, S3 and S4 are statements, a 4-case analysis
statement has the form,
case C1
S1
case C2
S2
case C3
S3
else
S4
The conditions C1, C2, and C3 are
evaluated in turn. For the first condition that evaluates to true, the
corresponding statement is executed, and the case analysis statement ends. If
none of the conditions evaluates to true, then the default case S4 is executed.
1.
The
cases are exhaustive: at least one of the cases is true. If all conditions are
false, the default case is true.
2.
The
cases are disjoint: only one of the cases is true. Though it is possible for
more than one condition to be true, the case analysis always executes only one
case, the first one that is true. If the three conditions are disjoint, then
the four cases are (1) C1, (2) C2, (3) C3, (4) (not C1) and (not C2) and (not
C3).
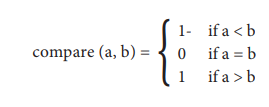
We can split the state into an
exhaustive set of 3 disjoint cases: a < b, a = b, and a> b. Then we can
define compare() using a case analysis.
1.
compare(a, b)
2.
case a < b
3.
result := -1
4.
case a = b
5.
result := 0
6.
else -- a > b
7.
result : = 1
4. Iterative statement
An iterative process executes the
same action repeatedly, subject to a condition C. If C is a condition and S is
a statement, then
while C
S
is a statement, called an iterative
statement, that describes the following action:
1.
Test
whether C is true or false.
2.
If C
is true, then do S and go back to step 1; otherwise do nothing.
The iterative statement is
commonly known as a loop. These two steps, testing C and executing S, are
repeated until C becomes false. When C becomes false, the loop ends, and the
control flows to the statement next to the iterative statement. The condition C
and the statement S are called the loop condition and the loop body,
respectively. Testing the loop condition and executing the loop body once is
called an iteration. not C is known as the termination condition.
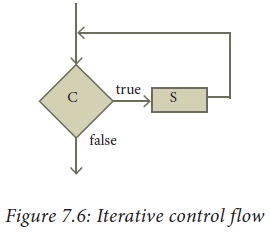
Iterative control flow is depicted
in the flowchart of Figure 7.6. Condition C has two outgoing arrows, true and
false. The true arrow points to S box. If C is true, S box is executed and
control flows back to C box. The false arrow points to the box after the
iterative statement (dotted box). If C is false, the loop ends and the control
flows to the next box after the loop.
Example 7.4. Construct an iterative algorithm to compute the quotient
and remainder after dividing an integer A by another integer B.
We formulated the specification of
the algorithm in Example 6.6 as
divide (A , B)
-- inputs: A is an integer and B ≠ 0
--outputs : q and r such
that A = q X B + r and
--0 ≤ r < B
Now we can construct an iterative
algorithm that satisfies the specification.
divide (A , B)
--inputs: A is an integer and B ≠ 0
--outputs : q and r such that A = q X B + r and
--0 < r < B
q := 0, A
while r ≥ B
q, r := q + 1, r - B
The algorithm is presented as a
flowchart in Figure 7.1.
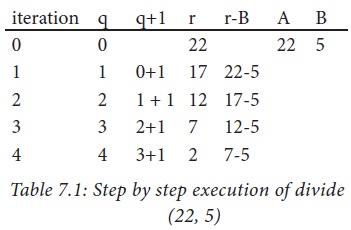
We can execute the algorithm
step-by-step for a test input, say, (A, B) = (22, 5). Each row of Table 7.1
shows one iteration — the evaluation of the expressions and the values of the
variables at the end of an iteration. Note that the evaluation of the
expression uses the values of the variables from the previous row. Output
variables q and r change their values in each iteration. Input variables A and
B do not change their values. Iteration 0 shows the values just before the loop
starts. At the end of iteration 4, condition (r ≥ B) = (2 ≥ 5) is
false, and hence the loop ends with (q, r) = (4, 2).
Example 7.5. In the Chameleons of Chromeland problem of Example 1.3,
suppose two types of chameleons are equal in number. Construct an algorithm
that arranges meetings between these two types so that they change their color
to the third type. In the end, all should display the same color.
Let us represent the number of
chameleons of each type by variables a, b and c, and their initial values by A,
B and C, respectively. Let a = b be the input property. The input-output
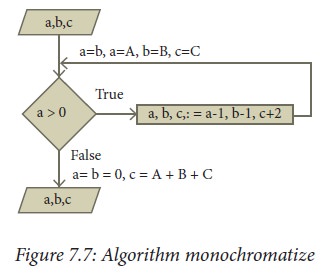
relation is a = b = 0 and c = A+B+C. Let us name the algorithm monochromatize.
The algorithm can be specified as
monochromatize(a, b, c)
--inputs: a=A, b=B, c=C, a=b
--outputs : a = b = 0 , c = A+B+C
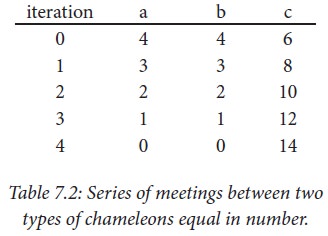
In each iterative step, two
chameleons of the two types (equal in number) meet and change their colors to
the third one. For example, if A, B, C = 4, 4, 6, then the series of meetings
will result in
In each meeting, a and b each decreases by 1, and c increases by 2. The solution can be expressed as an iterative algorithm.
monochromatize(a, b, c)
--inputs: a=A, b=B, c=C, a=b
--outputs: a = b = 0, c = A+B+C
while a > 0
a, b, c := a-1, b-1, c+2
The algorithm is depicted in the
flowchart of Figure 7.7.
Related Topics