Conics

Conics

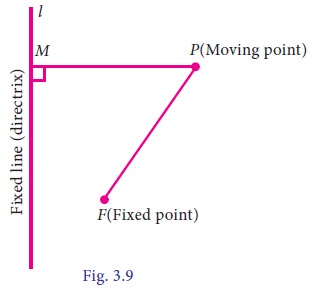
In figure, the fixed point F is called focus, the fixed straight line l is called directrix and P is the moving point such that FP/PM = e, a constant. Here the locus of P is called a conic and the constant ‘e’ is called the eccentricity of the conic.

1. Parabola

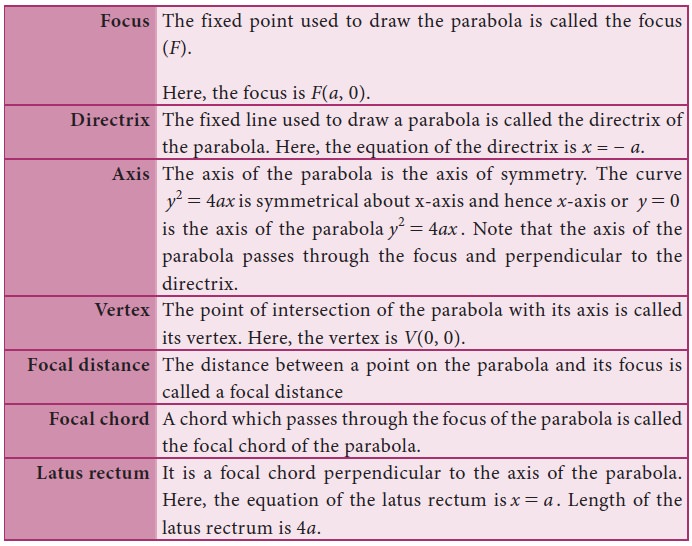
2. Definitions regarding a parabola: y 2 = 4ax

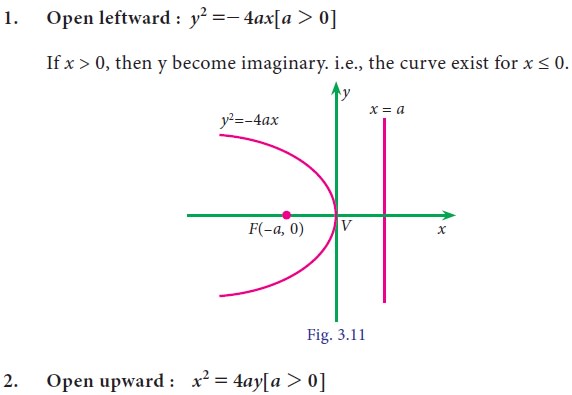
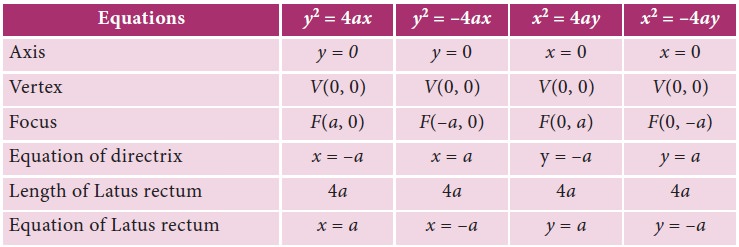
3. Other standard parabolas :

The process of shifting the origin or translation of axes.

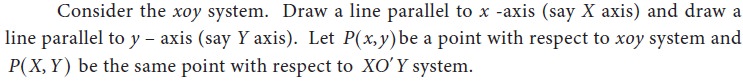
4. General form of the standard equation of a parabola, which is open rightward (i.e., the vertex other than origin) :

Consider a parabola with vertex V whose co-ordinates with respect to XOY system is (0, 0) and with respect to xoy system is (h, k). Since it is open rightward, the equation of the parabola w.r.t. XOY system is Y² = 4aX .