Definition, Formula, Solved Example Problems, Exercise | Mathematics - System of straight lines | 11th Business Mathematics and Statistics(EMS) : Chapter 3 : Analytical Geometry
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 3 : Analytical Geometry
System of straight lines
In lower classes, we studied the basic concept of coordinate geometry, like distance formula, section - formula, area of triangle and slope of a straight lines etc.
System of straight lines
We also studied various form of equations of lines in X std. Let us recall the equations of straight lines. Which will help us for better understanding the new concept and definitions of XI std co-ordinate geometry.
Equation of straight line having slope m and y-intercept ‘c’ is y = mx+c
ii. Point- slope form
Equation of Straight line passing through the given point P (x1 , y1) and having a slope m is

iii. Two-Point form

i. Intercept form
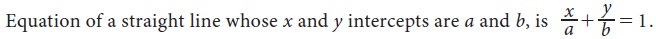
ii. General form
Equation of straight line in general form is ax + by + c = 0 where a, b and c are constants and a, b are not simultaneously zero.
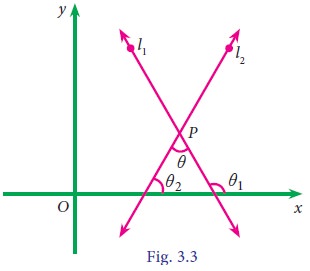
If θ1 and θ 2 are two angles made by l1 and l2 with x- axis then slope of the lines are m1 = tan θ 1 and m2 = tan θ 2 .
From fig 3.3, if i is angle between the lines l1 & l2 then
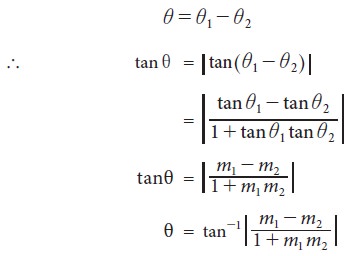

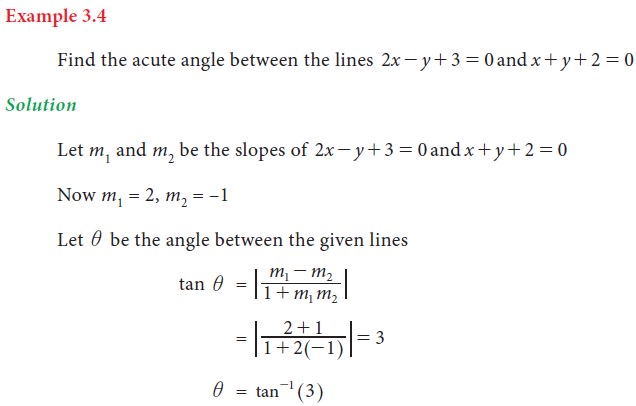


If three or more straight lines will have a point in common then they are said to be concurrent.
The lines passing through the common point are called concurrent lines and the common point is called concurrent point.
Conditions for three given straight lines to be concurrent



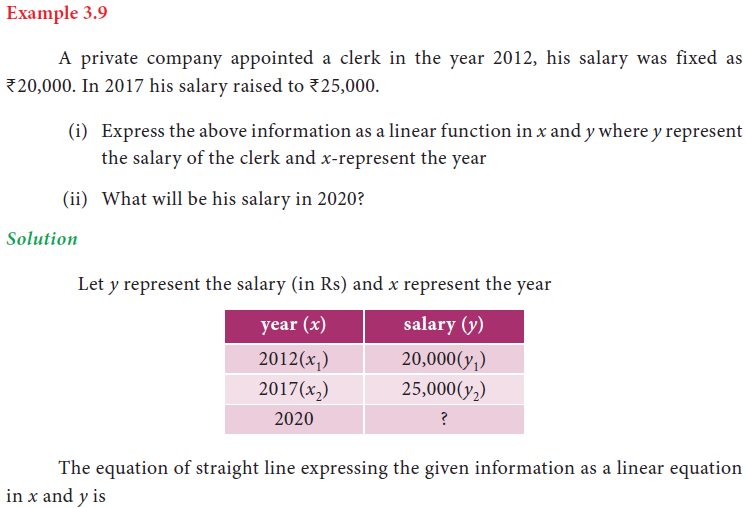
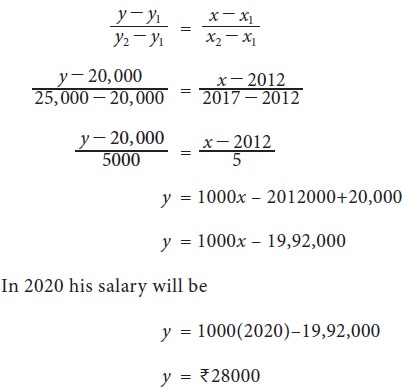

1. Recall
In lower classes, we studied the basic concept of coordinate geometry, like distance formula, section - formula, area of triangle and slope of a straight lines etc.We also studied various form of equations of lines in X std. Let us recall the equations of straight lines. Which will help us for better understanding the new concept and definitions of XI std co-ordinate geometry.
Various forms of straight lines:
i. Slope-intercept formEquation of straight line having slope m and y-intercept ‘c’ is y = mx+c
ii. Point- slope form
Equation of Straight line passing through the given point P (x1 , y1) and having a slope m is

iii. Two-Point form

i. Intercept form
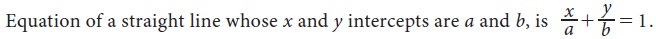
ii. General form
Equation of straight line in general form is ax + by + c = 0 where a, b and c are constants and a, b are not simultaneously zero.
2. Angle between two straight lines
Let l1 and l2 be two straight lines represented by the equations l1: y = m1 x + c1 and l2: y = m2 x + c2 intersecting at P.If θ1 and θ 2 are two angles made by l1 and l2 with x- axis then slope of the lines are m1 = tan θ 1 and m2 = tan θ 2 .
From fig 3.3, if i is angle between the lines l1 & l2 then

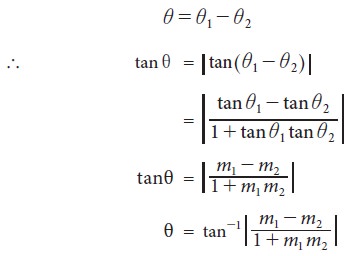

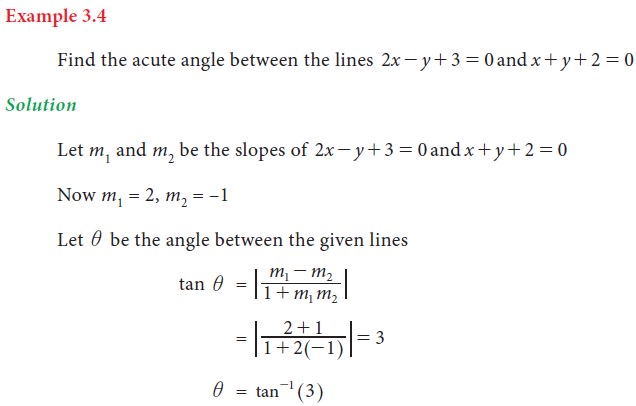
3. Distance of a point from a line


4. Concurrence of three lines
If two lines l1 and l2 meet at a common point P, then that P is called point of This intersection of l1 and l2 . point of intersection is obtained by solving the equations of l1 and l2 .If three or more straight lines will have a point in common then they are said to be concurrent.
The lines passing through the common point are called concurrent lines and the common point is called concurrent point.
Conditions for three given straight lines to be concurrent




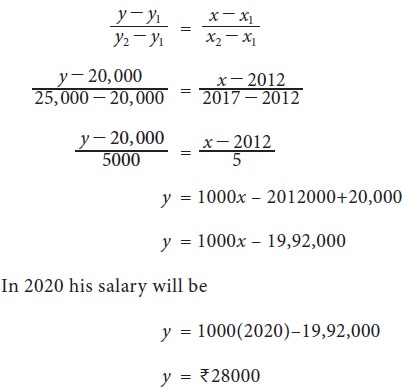

Tags : Definition, Formula, Solved Example Problems, Exercise | Mathematics , 11th Business Mathematics and Statistics(EMS) : Chapter 3 : Analytical Geometry
Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
11th Business Mathematics and Statistics(EMS) : Chapter 3 : Analytical Geometry : System of straight lines | Definition, Formula, Solved Example Problems, Exercise | Mathematics
Related Topics
11th Business Mathematics and Statistics(EMS) : Chapter 3 : Analytical Geometry