Configurational isomers - optical isomers

CONFIGURATIONAL ISOMERS – OPTICAL ISOMERS

Key Notes

Definition

Optical isomers are configurational isomers which have the ability to rotate plane-polarized light clockwise or counterclockwise. They have identical chemical and physical properties (apart from their effects on plane-polarized light), but can have different biological properties.

Asymmetric molecules

Asymmetric molecules are molecules which lack symmetry. Such molecules can also be termed as chiral molecules and as such can exist as two non-superimposable mirror images. These mirror images are optical isomers and are a form of configurational isomerism. Complete asymmetry is not required for a molecule to be chiral and some chiral molecules can have a single axis of symmetry.

Asymmetric carbon centers

Asymmetric carbon centers are carbon atoms having four different sub-stituents. Molecules having asymmetric centers will usually be chiral. How-ever, there are special cases where molecules can have asymmetric centers and be achiral, or where molecules are chiral but have no asymmetric cen-ters. Nonsuperimposable mirror images of a molecule are called enan-tiomers. An equal mixture of two enantiomers is called a racemate and does not rotate plane polarized light. Asymmetric carbon centers are only possi-ble on sp³ carbons.

Fischer diagrams

Fischer diagrams are used to represent chiral molecules. The vertical bonds in a Fischer diagram represent bonds pointing into the page while the horizontal bonds represent bonds coming out of the page.

R and S nomenclature

The R and S nomenclature is used to determine the absolute configuration at asymmetric centers. The groups attached to the asymmetric center are given priorities based on the atomic weights of the atoms directly attached to the center. The group of lowest priority is placed behind the page and an arc is drawn connecting the top three priority groups. If the arc is clockwise, the assignment is R. If the arc is anticlockwise, the assignment is S.

(+) and (–)

The symbols (+) and (-) are used to show which direction an enantiomer rotates plane-polarized light. The direction of rotation can only be deter-mined by experimentation.

Optical purity

Optical purity is quoted in terms of enantiomeric excess. This indicates the excess of pure enantiomer over racemate.

Allenes and spiro compounds

Some substituted allenes and spiro compounds are chiral molecules despite the lack of an asymmetric center. Molecules are chiral if they are asymmet-ric overall or contain only one axis of symmetry.

meso structures

A meso structure has two identical asymmetric centers which effectively cancel each other out. Such a molecule has a plane of symmetry and cannot be chiral. The mirror images are superimposable and optical isomers are not possible.

Diastereomers

Molecules containing more than one asymmetric center can have several stereoisomers, that is, different configurational isomers. For each asymmet-ric center present (n) in a molecule, there are 2ⁿ possible stereoisomers. Every stereoisomer has a mirror image and so there are 2^n-1 sets of enan-tiomers. Each set of enantiomers is called a diastereomer. Diastereomers are different molecules having different chemical and physical properties.

Definition

Optical isomerism is another example of configurational isomerism and is so named because of the ability of optical isomers to rotate plane-polarized light clockwise or counterclockwise. The existence of optical isomers has very important  consequences  for  life,  since  optical  isomers  often  have  significant differences in their biological activity. Apart from their biological activity and their effects  on  plane-polarized  light,  optical  isomers  have  identical  chemical  and physical properties.

Asymmetric molecules

A molecule such as chloroform (CHCl₃) is tetrahedral and there is only one way of fitting the atoms together. This is not the case for a molecule such as lactic acid.

There are two ways of constructing a model of lactic acid, such that the two struc- tures  obtained  are  nonsuperimposable  and  cannot  be  interconverted  without breaking covalent bonds. As such, they represent two different molecules which are configurational isomers. The difference between the two possible molecules lies in the way the substituents are attached to the central carbon. This can be rep- resented by the following drawings (Fig. 1) where the bond to the hydroxyl group comes out of the page in one isomer but goes into the page in the other isomer.

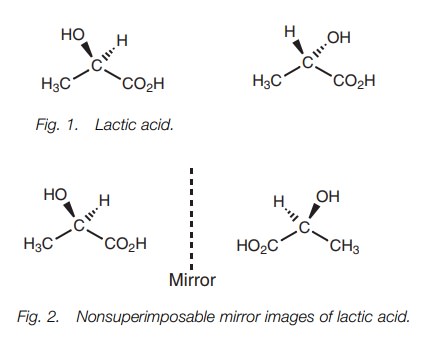
The two isomers of lactic acid are mirror images (Fig. 2). A molecule which exists as two nonsuperimposable mirror images has optical activity if only one of the mirror images is present.

Lactic acid exists as two nonsuperimposable mirror images because it is asym- metric – in other words it lacks symmetry. Asymmetric molecules can also betermed as chiral, and the ability of molecules to exist as two optical isomers iscalled chirality. In fact, a molecule does not have to be totally asymmetric to bechiral. Molecules containing a single axis of symmetry can also be chiral.

Asymmetric carbon centers

A simple method of identifying most chiral molecules involves identifying what are known as asymmetric carbon centers. This works for most chiral molecules ,but it is important to realize that it is not foolproof and that there are several cases where it will not work. For example, some chiral molecules have no asymmetric carbon centers, and some molecules having more than one asymmetric carbon center are not chiral.

Usually, a compound will have optical isomers if there are four different sub- stituents attached to a central carbon (Fig. 3). In such cases, the mirror images are nonsuperimposable and the structure will exist as two configurational isomers called enantiomers. The carbon center which contains these four different sub- stituents is known as a stereogenic or an asymmetric center. A solution of each enantiomer or optical isomer is capable of rotating plane-polarized light. One enantiomer will rotate plane-polarized light clockwise while the other (the mirrorimage) will rotate it counterclockwise by the same amount. A mixture of the two isomers  (a  racemate)  will  not  rotate  plane-polarized  light  at  all.  In  all  other respects, the two isomers are identical in physical and chemical properties and aretherefore  indistinguishable.  The  asymmetric  centers  in  the  molecules  shown(Fig. 4) have been identified with an asterisk. The structure lacking the asymmetriccenter is symmetric or achiral and does not have optical isomers. A structure canalso have more than one asymmetric center.

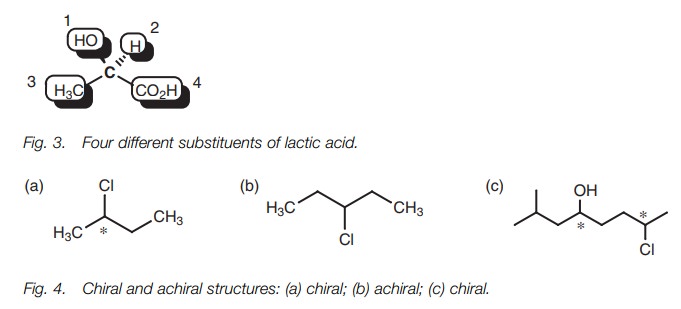
Asymmetric centers are only possible on sp³ carbons. Ansp² center is planar and cannot be asymmetric. Similarly, ansp center cannot be asymmetric.

Fischer diagrams

A chiral molecule can be represented by a Fischer diagram (Fig. 5). The molecule is  drawn  such  that  the  carbon  chain  is  vertical  with  the  functional  group positioned at the top. The vertical C–C bonds from the asymmetric center point into the page while the horizontal bonds from the asymmetric center come out of the page. This is usually drawn without specifying the wedged and hatched bonds.

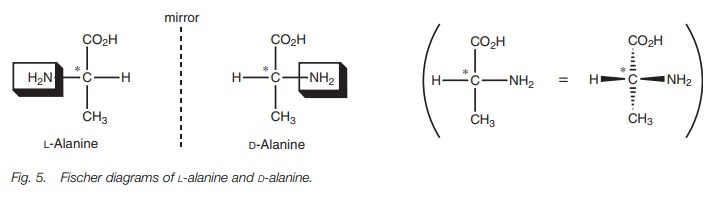
The Fischer diagrams of alanine allow the structures to be defined as L- or D- from the position of the amino group. If the amino group is to the left, then it is the L- enantiomer. If it is positioned to the right, it is the D-enantiomer. This is an old fashioned nomenclature which is only used for amino acids and sugars. The L- and D- nomenclature depends on the absolute configuration at the asymmetric center and not the direction in which the enantiomer rotates plane-polarized light. It is not possible to predict which way a molecule will rotate plane-polarized light and this can only be found out by experimentation.

R and S nomenclature

The structure of an enantiomer can be specified by the R and S nomenclature, determined by the Cahn–Ingold–Prelog rules. The example (Fig. 6) shows how the nomenclature is worked out. First of all, the atoms directly attached to the asym- metric center and their atomic numbers are identified. Next, you give the attached atoms a priority based on their atomic numbers. In this example, there are two car- bon atoms with the same atomic numbers and so they cannot be given a priority. When this happens, the next stage is to move to the next atom of highest atomic number (Fig. 7a). This means moving to an oxygenfor one of the carbons and to a hydrogen for the other.

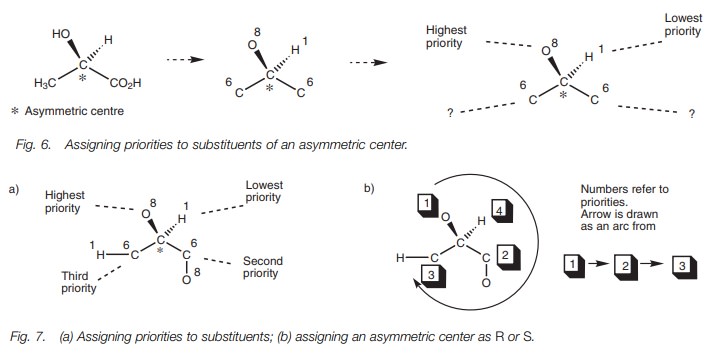
The oxygen has the higher priority and so this substituent takes priority over the other. Once the priorities have been settled, the structure is redrawn such that the group of lowest priority is positioned ‘behind the page’. 

In this example (Fig. 7b), the group of lowest priority (the hydrogen) is already positioned behind the page (note the hatched bond indicating the bond going away from you). An arc is now drawn connecting the remaining groups, starting from the group of highest priority and finishing at the group of third priority. If the arc is drawn clockwise, the assignment is R (rectus). If the arc is drawn counterclockwise, the assignment is S (sinister). In this example the arrow is drawn clockwise. Therefore, the molecule is (R)-lactic acid.

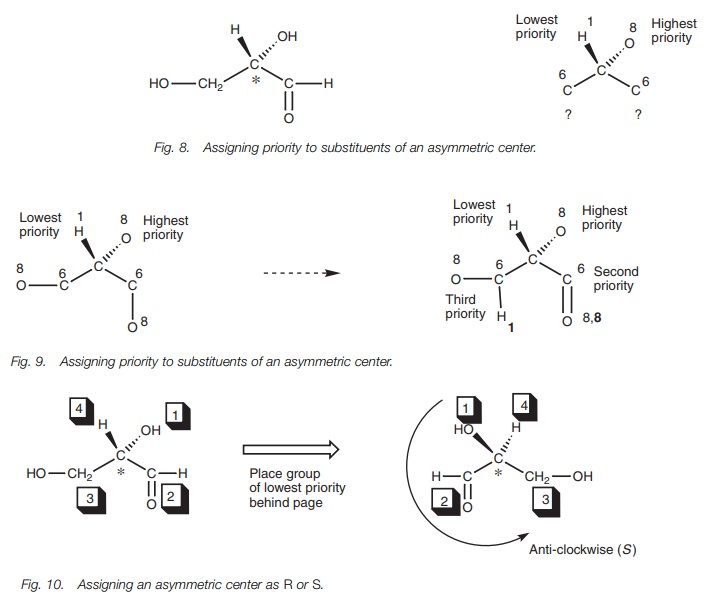
A second example (Fig. 8) illustrates another rule involving substituents with double bonds. The asymmetric center is marked with an asterisk. The atoms directly attached to the asymmetric center are shown on the right with their atomic numbers. At this stage, it is possible to define the group of highest priority (the oxygen) and the group of lowest priority (the hydrogen). There are two iden-tical carbons attached to the asymmetric center so we have to move to the next stage and identify the atom with the highest atomic number joined to each of the identical carbons (Fig. 9). This still does not distinguish between the CHO and CH₂OH groups since both carbon atoms have an oxygen atom attached. The next stage is to look at the second most important atom attached to the two carbon atoms. However, if there is a double bond present, you are allowed to ‘visit’ the same atom twice. The next most important atom in the CH₂OH group is the hydrogen. In the CHO group, the oxygen can be ‘revisited’ since there is a double bond. Therefore, this group takes priority over the CH₂OH group. The priorities have been determined, and so the group of lowest priority is placed behind the page and the three most important groups are connected to see if they are clock-wise or counterclockwise (Fig. 10).

(+) and (–)

The assignment of an asymmetric center as R or S has nothing to do with whichever direction the molecule rotates plane-polarized light. Optical rotation can only be determined experimentally. By convention, molecules which rotate plane-polarized light clockwise are defined as (+) or d. Molecules which rotate plane-polarized light counterclockwise are defined as (-) or l. The R enantiomer of lactic acid is found to rotate plane-polarized lightcounterclockwise and so this molecule is defined as (R)-( )-lactic acid.

Optical purity

The optical purity of a compound is a measure of its enantiomeric purity and is given in terms of its enantiomeric excess (ee). A pure enantiomer would have an optical purity and enantiomeric excess of 100%. A fully racemized compound would have an optical purity of 0%. If the enantiomeric excess is 90%, it signifies that 90% of the sample is pure enantiomer and the remaining 10% is a racemate containing equal amounts of each enantiomer (i.e. 5% + 5%). Therefore the ratio of enantiomers in a sample having 90% optical purity is 95:5.

Allenes and spirocompounds

Not all chiral molecules have asymmetric centers. For example, some substituted  allenes and spiro structures have no asymmetric center but are still chiral (Fig. 11). The substituents at either end of the allene are in different planes, and the rings in the spiro structure are at right angles to each other. The mirror images of the allene and the spiro structures are nonsuperimposable and are enantiomers.

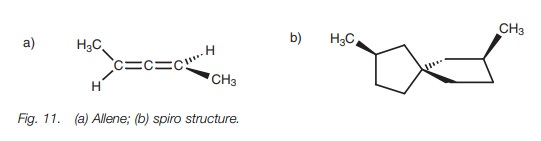
A better rule for determining whether a molecule is chiral or not is to study the symmetry of the molecule. A molecule will be chiral if it is asymmetric (i.e. has no elements of symmetry) or if it has no more than one axis of symmetry.

mesostructures

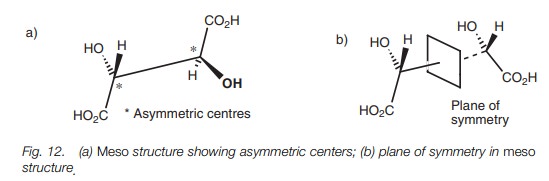
The molecule in Fig. 12a has two identical asymmetric centers but is not chiral. The mirror images of this structure are superimposable and so the compound cannot be chiral. This is because the molecule contains a plane of symmetry as demonstrated in Fig. 12b where the molecule has been rotated around the central C–C bond. A structure such as this is called a meso structure.

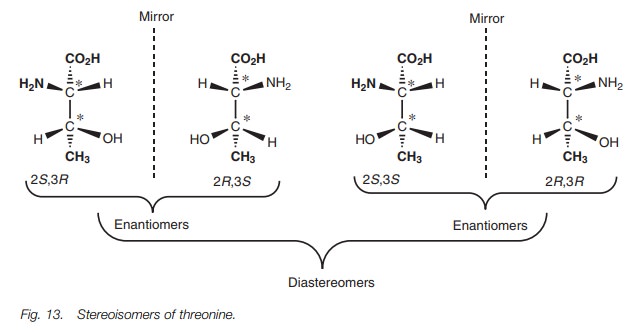
Diastereomers

Whenever a molecule has two or more asymmetric centers, there are several possible structures which are possible and we need to use terms such as stereoisomers, diastereomers and enantiomers in order to discuss them. To illustrate the relativemeaning of these terms, we shall look at the possible structures of the amino acid threonine (Fig. 13). This molecule has two asymmetric centers. As a result, four different structures are possible arising from the two different possible configurations at each center. These are demonstrated with the asymmetric centers at positions 2 and 3 defined as R or S. The four different structures are referred to as stereoisomers. The (2S,3R) stereoisomer is a nonsuperimposable mirror image of the (2R,3S) stereoisomer and so these structures are enantiomers having the same chemical and physical properties. The (2S,3S) stereoisomer is the nonsuperimposable mirror image of the (2R,3R) stereoisomer and so these structures are also enantiomers having the same chemical and physical properties. Each set of enantiomers is called a diastereomer. Diastereomers are not mirror images of each other and are completely different compounds having different physical and chemical properties. To conclude, threonine has two asymmetric centers which means that there are two possible diastereomers consisting of two enantiomers each, making a total of four stereoisomers. As the number of asymmetric centers increases, the number of possible stereoisomers and diastereomers increases. For a molecule having n asymmetric centers, the number of possible stereoisomers is 2ⁿ and the number of diastereomers is 2^n-1.