Concept of Self-GMD and Mutual-GMD

CONCEPT OF SELF-GMD AND MUTUAL-GMD

The use of self geometrical mean distance (abbreviated as self-GMD) and mutual geometrical mean distance (mutual-GMD) simplifies the inductance calculations, particularly relating to multi conductor arrangements. The symbols used for these are respectively Ds and Dm. We shall briefly discuss these terms.

( i) Self-GMD (Ds)

In order to have concept of self-GMD (also sometimes called Geometrical mean radius; GMR), consider the expression for inductance per conductor per metre already derived in Art. Inductance/conductor/m

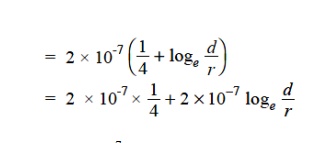
In this expression, the term 2 × 10-7 × (1/4) is the inductance due to flux within the solid conductor. For many purposes, it is desirable to eliminate this term by the introduction of a concept called self-GMD or GMR. If we replace the original solid conductor by an equivalent hollow cylinder with extremely thin walls, the current is confined to the conductor surface and internal conductor flux linkage would be almost zero. Consequently, inductance due to internal flux would be zero and the term 2 × 10-7 × (1/4) shall be eliminated. The radius of this equivalent hollow cylinder must be sufficiently smaller than the physical radius of the conductor to allow room for enough additional flux to compensate for the absence of internal flux linkage. It can be proved mathematically that for a solid round conductor of radius r, the self-GMD or GMR = 0·7788 r. Using self-GMD, the eq. ( i) becomes :

Inductance/conductor/m = 2 × 10-7loge d/ Ds *

Where

Ds = GMR or self-GMD = 0·7788 r

It may be noted that self-GMD of a conductor depends upon the size and shape of the conductor and is independent of the spacing between the conductors.

(ii) Mutual-GMD

The mutual-GMD is the geometrical mean of the distances form one conductor to the other and, therefore, must be between the largest and smallest such distance. In fact, mutual-GMD simply represents the equivalent geometrical spacing.

(a)     The mutual-GMD between two conductors (assuming that spacing between conductors is large compared to the diameter of each conductor) is equal to the distance between their centres i.e. Dm = spacing between conductors = d

(b)  For a single circuit 3-φ line, the mutual-GMD is equal to the equivalent equilateral spacing i.e., ( d1 d2 d3 )1/3.

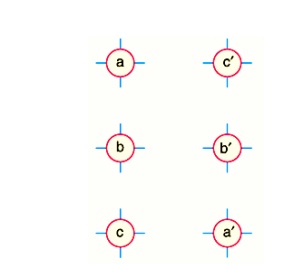
(c) The principle of geometrical mean distances can be most profitably employed to 3-φ double circuit lines. Consider the conductor arrangement of the double circuit shown in Fig. Suppose the radius of each conductor is r.

Self-GMD of conductor = 0·7788 r

Self-GMD of combination aa’ is

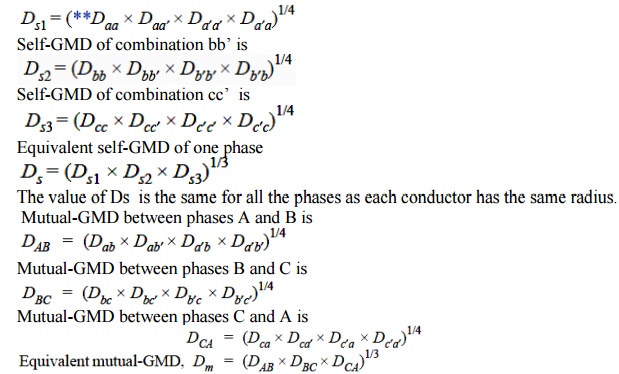
It is worthwhile to note that mutual GMD depends only upon the spacing and is substantially independent of the exact size, shape and orientation of the conductor.

Inductance Formulas in Terms of GMD

The inductance formulas developed in the previous articles can be conveniently expressed in terms of geometrical mean distances.