Classification of system

Classification of system:

The systems are classified as,

·              Static & dynamic system

·              Time invariant and variant system

·              Linear and non linear system

·              Causal and non causal system

·              Stable and unstable system

1. Static and dynamic system:

·              Static system is said to be a memoryless system.

·              The output does not depend the past or future input.

·              It only depends the present input for an output.

Eg, y(n) = x(n)

·              Dynamic system is said to be as system with memory.

·              Its output depend the past values of input for an output.

Eg.Y(n) = x(n) + x(n - 1)

·              This static and dynamic systems are otherwise called as memoryless and system with memory.

2. Systems with and without memory:

A system is called memory less if the output at any time t (or n) depends only on the input at time t (or n); in other words, independent of the input at times before of after t (or n). Examples of memory less systems:

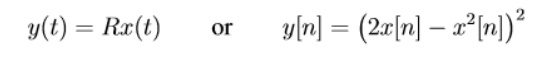
Examples of systems with memory:

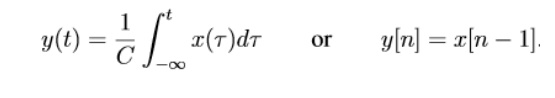
3. Time invariant and time variant system:

If the time shifts in the input signals results in corresponding time shift in the output, then the system is called as time invariant.

The input and output characteristics do not change with time.

f[x(t₁ – t₂)] = y(t₁ – t₂)

For a continuous time system,

f[x(t₁ – t₂)] = y(t₁ – t₂)

For a discrete time system,

F[x(n - k)] = y(n - k)

If the above relation does not satisfy, then the system is said to be a time variant system.

A system is called time-invariant if the way it responds to inputs does not change over time:

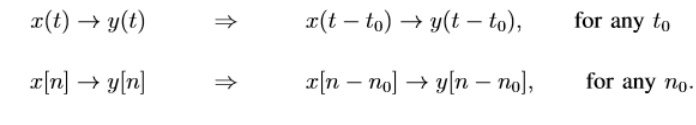
Examples of time-invariant systems:

The RC circuit considered earlier provided the values of R or C are constant.

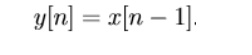
Examples of time-varying systems:

The RC circuit considered earlier if the values of R or C change over time.

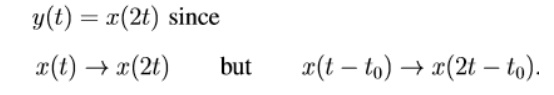
Most physical systems are slowly time-varying due to aging, etc. Hence, they can be considered time-invariant for certain time periods in which its behavior does not change significantly.

4. Linear and non linear system:

A system is said to be linear if it satisfies the superposition principle.

Superposition principle states that the response to a weighted sum of input signal be equal to the weighted sum of the output corresponding to each of the individual input signal

The continuous system is linear if,

F[a₁x₁(t) + a₂x₂(t)] = a₁y₁(t) + a₂y₂(t)

The discrete system is linear if,

F[a₁x₁(n) + a₂x₂(n)] = a₁y₁(n) + a₂y₂(n)

Otherwise the system is non linear.

A system is called linear if its I/O behavior satisfies the additivity and homogeneity properties:

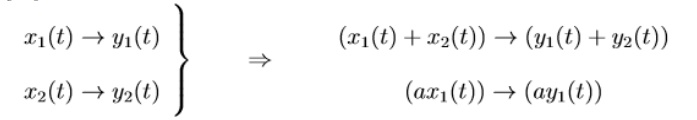
for any complex constant a.

Equivalently, a system is called linear if its I/O behavior satisfies the superposition property:

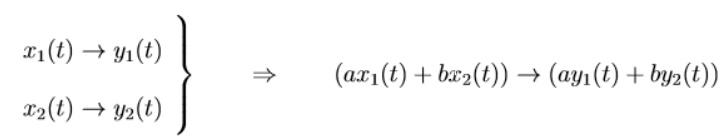
where any complex constants a and b.

5. Causal and non causal system:

A causal system is one whose output depends upon the present and past input values.

If the system depends the future input values, the system is said to be non causal. Eg.for causal system.

Y(t) = x(t) + x(t - 1)

Y(n) = x(n) + x(n - 3)

Eg. For non causal system,

Y(t) = x(t+3) + x2(t)

Y(n) = x(2n)

A system is called causal or non-anticipative if the output at any time t (or n) depends only on the input at times t or before t (or n or before n); in other words, independent of the input at times after t (or n). All memory less systems are causal. Physical systems where the time is the independent variable are causal.

Non-causal systems may arise in applications where the independent variable is not the time such as in the image processing applications.

Examples of causal systems:

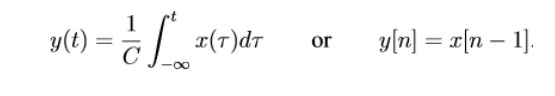
Examples of non-causal systems:

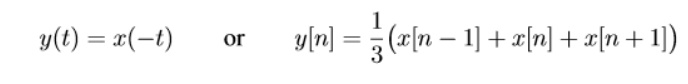
6. Stable and unstable system:

When every bounded input produces bounded output then the system is called as stable system or bounded input bounded output (BIBO stable).

Otherwise the system is unstable.

A system is called stable if it produces bounded outputs for all bounded inputs

Stability in a physical system generally results from the presence of mechanisms that dissipate energy, such as the resistors in a circuit, friction in a mechanical system, etc