Boolean Algebra

Boolean Algebra

Introduction

Boolean algebra is a mathematical discipline that is used for designing digital circuits in a digital computer. It describes the relation between inputs and outputs of a digital circuit. The name Boolean algebra has been given in honor of an English mathematician George Boole who proposed the basic principles of this algebra.

1. Binary valued quantities:

Every day we have to make logical decisions:

1. Should I carry Computer Science book every day? Yes / No

2. 8-10 = 10 is this answer correct? Yes / No

3. Chennai is capital of India? Yes / No

4. What did I say yesterday?

The first three questions thrown above, the answer may be True (Yes) or False (No). But the fourth one, we cannot be answer as True or False. Thus, sentences which can be determined to be True or False are called “Logical Statement” or “Truth Functions”. The results True or False are called “Truth Values”. The truth values depicted by logical constant 1 and 0; 1 means True and 0 means False. The variable which can store these truth values are called “Logical variable” or “Binary valued variables” or “Boolean Variables” as these can store one of the two values of True or False.

2. Logical Operations:

Boolean algebra makes use of variables and operations (functions). The basic logical operations are AND, OR and NOT, which are symbolically represented by dot ( . ), plus ( + ), and by over bar / single apostrophe respectively. These symbols are also called as “Logical Operators”.

3. Truth Table:

A truth table represents all the possible values of logical variable or statements along with all the possible results of given combination of truth values.

4. AND operator

The AND operator is defined in Boolean algebra by the use of the dot (.) operator. It is similar to multiplication in ordinary algebra. The AND operator combines two or more input variables so that the output is true only if all the inputs are true. The truth table for a 2-input AND operator is shown as follows:

The above 2-input AND operation is expressed as: Y = A . B

5. OR operator

The plus sign is used to indicate the OR operator. The OR operator combines two or more input variables so that the output is true if at least one input is true. The truth table for a 2-input OR operator is shown as follows:

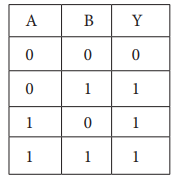
The above 2-input OR operation is expressed as: Y = A + B

6. NOT operator

The NOT operator has one input and one output. The input is either true or false, and the output is always the opposite, that is, the NOT operator inverts the input. The truth table for a NOT operator where A is the input variable and Y is the output is shown below:

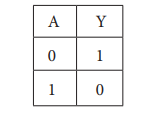
The NOT operator is represented algebraically by the Boolean expression: 

Otherwise D is equal to 0 (false).

The basic logic functions AND, OR, and NOT can also be combined to make other logic operators such as NAND and NOR

7. NAND operator

The NAND is the combination of NOT and AND. The NAND is generated by inverting the output of an AND operator. The algebraic expression of the NAND function is:

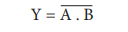
The NAND function truth table is shown below:

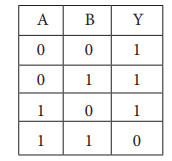
A NAND B = NOT (A AND B)

8  NOR operator

The NOR is the combination of NOT and OR. The NOR is generated by inverting the output of an OR operator. The algebraic expression of the NOR function is:

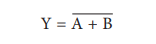
The NOR function truth table is shown below:

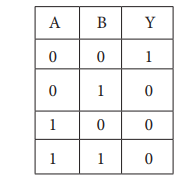
A NOR B = NOT (A OR B)