Answer the following questions

Fundamentals of Computers

Boolean Algebra

Evaluation

PART – II

1. What is Boolean Algebra?

Answer: Boolean algebra is a mathematical discipline that is used for designing digital circuits in a digital computer. It describes the relation between inputs and outputs of a digital circuit. Example : X = A +B.

2. Write a short note on NAND Gate.

Answer: (i) The NAND gate operates an AND gate followed by a NOT gate.

(ii) It acts in the manner of the logical operation "AND" followed by inversion. The output is "false" if both inputs are "true", otherwise, the output is "true".

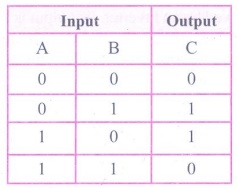
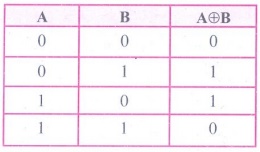
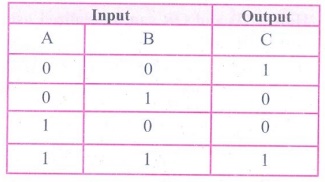
3. Draw the truth table for XOR gate.

Answer: The truth table for XOR gate is

4. Write the associative laws?

Answer: Associative

A + (B + C) = (A + B) + C

 A. (B . C) = (A . B). C

5. What are derived gates?

Answer: NAND, NOR, XOR and XNOR are derived gates which are derived from the fundamental logical gates.

Part – III

1.  Write the truth table of fundamental gates.

Answer:

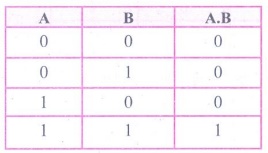
(i) AND Gate Truth Table :

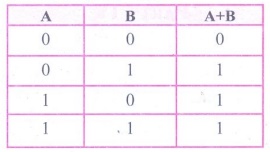
(ii) OR Gate Truth Table :

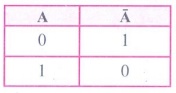
(iii) NOT Gate Truth Table :

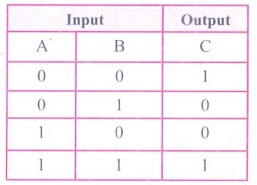
2. Write a short note on XNOR gate.

Answer: The XNOR (exclusive - NOR) gate is a combination XOR gate followed by an inverter. Its output is "true" if the inputs are the same, and "false" if the inputs are different. In simple words, the output is 1 if the input are the same, otherwise the output is 0.

The truth table for XNOR Gate is

3. Reason out why the NAND an NOR are called universal gates?

Answer: NAND and NOR gates are called Universal gates, because the fundamental logic gates can be realized through them.

4. Give the truth table of XOR gate.

Answer:

5. Write the De Morgan’s law.

Answer: De Morgan’s

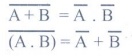
PART – IV

1. Explain the fundamental gates with expression and truth table.

Answer: A gate is basic electronic circuit which operates on one or more signals to produce an output signal. There are three fundamental gates namely AND, OR and NOT.

AND Gate :

The AND gate can have two or more input signals and produce an output signal. In boolean algebra, a variable can take either of the values '0' or '1'. The logical symbol of the AND gate is AND gate is

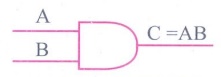
 Logic symbol of AND Gate

In boolean algebra the multiplication sign stands for the AND operation. Therefore, the output of the AND gate is

C = A . B or

simply C=AB

The truth table for AND Gate is

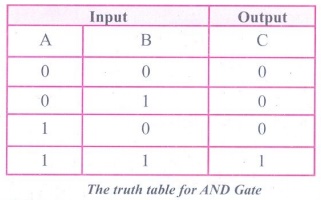
The truth table for AND Gate

OR Gate :

The OR gate gets its name from the face that it behaves like the logical inclusive "OR". The output is "true" if either or both of the inputs are "true". If both inputs are "false" then the output is "false". In otherwords the output will be 1 if and only if one or both inputs are 1; otherwise, the output is 0. The logical symbol of the OR gate is

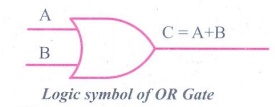
Logic symbol of OR Gate

The OR gate output is

C = A OR B

We use the + sign to denote the OR function.

Therefore,

C = A+ B 

The truth table for OR gate is

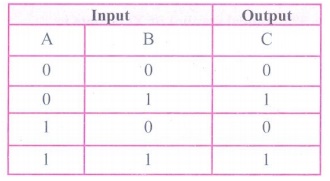
NOT Gate :

The NOT gate, called a logical inverter, has only one input. It reverses the logical state. In other words the output C is always the complement of the input. The logical symbol of the NOT gate is

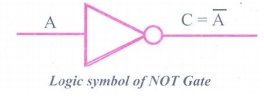
Logic symbol of NOT Gate

The boolean function of NOT gate is

C = NOT A

In boolean algebra, the overbar stands for NOT operation. Therefore, C = 

The truth table for NOT gate is

2. How AND and OR can be realized using NAND and NOR gate.

Answer:

(i) AND and OR operation from NAND gates are shown below.

NAND gates AND Operation:

A.B = (A NAND B) NAND (A NAND B)

OR Operation :

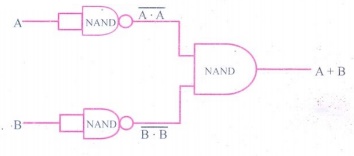
A+B (A NAND A) NAND (B NAND Y)

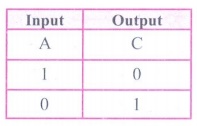
The truth table for NAND Gate is

 (ii) AND and OR operation from NOR gates are shown below.

NOR gates AND Operation :

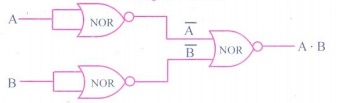
A − B = (A NORA A) NOR (B NOR B).

NOR gate OR Operation :

A +B = (A NOR B) NOR (A NOR B).

The truth table for NAND Gate is

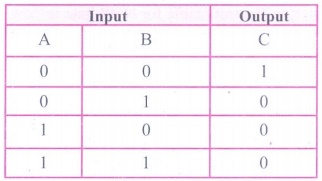
3. Explain the Derived gates with expression and truth table.

Answer: NAND, NOR, XOR and XNOR are derived gates which are derived from the fundamental gates.

(i) NAND Gate: The NAND gate operates an AND gate followed by a NOT gate. It acts in the manner of the logical operation "AND" followed by inversion. The output is "false" if both inputs are "true", otherwise, the output is "true"

The output of the NAND gate is C = 

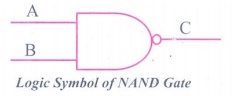
Logic Symbol of NAND Gate

The truth table for NAND gate is

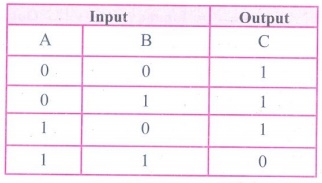
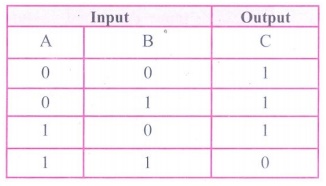
(ii) NOR Gate : The NOR gate circuit is an OR gate followed by an inverter. Its output is "true" if both inputs are "false" Otherwise, the output is "false".

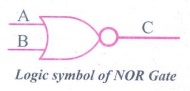
Logic symbol of NOR Gate

The output of NOR gate is C = 

Read this as "C equals NOT of A OR B" or "C equals the complement of A OR B".

The truth table for NOR gate is

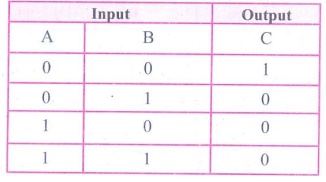
(iii) XOR Gate: The XOR (exclusive - OR) gate acts in the same way as the logical "either/or." The output is "true" if either, but not both, of the inputs are "true". The output is "false" if both inputs are "false" or if both inputs are "true." In boolean algebra, exclusive - OR operator  or "encircled plus".

Hence C = A  B

The logical symbol of XOR gate is

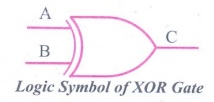
Logic Symbol of XOR Gate

The truth table of XOR gate is

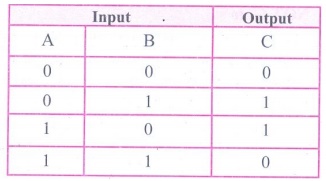
(iv) XNOR Gate : The XNOR (exclusive - NOR) gate is a combination XOR gate followed by an inverter.

The logical symbol of XNOR gate is

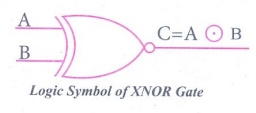
Logic Symbol of XNOR Gate

The truth table for XNOR Gate is