Basic Logic Gates

Basic Logic Gates:

A gate is a basic electronic circuit which operates on one or more signals to produce an output signal. There are three fundamental gates namely AND, OR and NOT. The other logic gates like NAND, NOR, XOR and XNOR are derived gates which are derived from the fundamental gates. NAND and NOR gates are called Universal gates, because the fundamental logic gates can be realized through them.

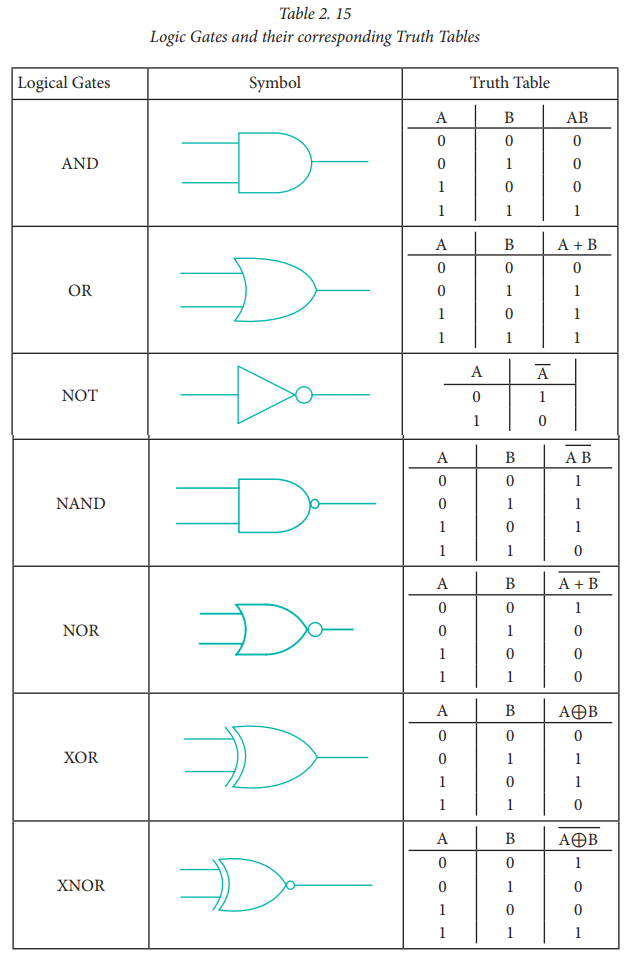
1. AND Gate

The AND gate can have two or more input signals and produce an output signal.

The output is "true" only when both inputs are "true", otherwise, the output is "false". In other words the output will be 1 if and only if both inputs are 1; otherwise the output is 0. The output of the AND gate is represented by avariable say C, where A and B are two and if input boolean variables. In boolean algebra, a variable can take either of the values '0' or '1'. The logical symobl of the AND gate is

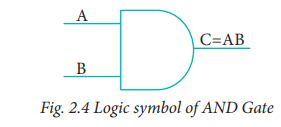
One way to symbolize the action of an AND gate is by writing the boolean function.

C = A AND B

In boolean algebra the multiplication sign stands for the AND operation. Therefore, the output of the AND gate is

C = A . B or

simply C = AB

Read this as "C equals A AND B". Since there are two input variables here, the truth table has four entries, because there are four possible inputs : 00, 01, 10 and 11.

For instance if both inputs are 0,

C = A . B

 =0 . 0

=0

The truth table for AND Gate is

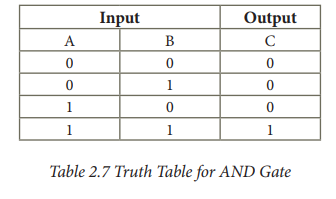
2.  OR Gate

The OR gate gets its name from its behaviour like the logical inclusive "OR". The output is "true" if either or both of the inputs are "true". If both inputs are "false" then the output is "false". In otherwords the output will be 1 if and only if one or both inputs are 1; otherwise, the output is 0. The logical symbol of the OR gate is

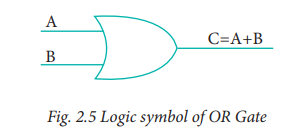
The OR gate output is

C = A OR B

We use the + sign to denote the OR function. Therefore,

C = A + B

Read this as "C equals A OR B".

For instance, if both the inputs are 1

C = A + B = 1 + 1 = 1

The truth table for OR gate is

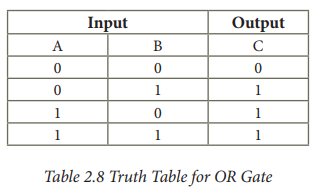
3.  NOT Gate

The NOT gate, called a logical inverter, has only one input. It reverses the logical state. In other words the output C is always the complement of the input. The logical symbol of the NOT gate is

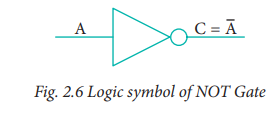
The boolean function of NOT gate is

C = NOT A

In boolean algerbra, the overbar stands for NOT operation. Therefore,

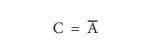
Read this as "C equals NOT A" or "C equals the complement of A".

If A is 0,

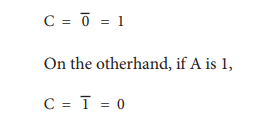
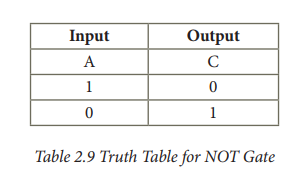
The truth table for NOT gate is

4.  NOR Gate

The NOR gate circuit is an OR gate followed by an an inverter. Its output is "true" if both inputs are "false" Otherwise, the output is "false". In other words, the only way to get '1' as output is to have both inputs '0'. Otherwise the output is 0. The logic circuit of the NOR gateis

5.  Bubbled AND Gate

The Logic Circuit of Bubbled AND Gate

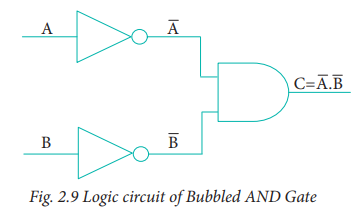
In the above circuit, invertors on the input lines of the AND gate gives the output as

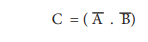
This circuit can be redrawn as the bubbles on the inputs, where the bubbles represent inversion.

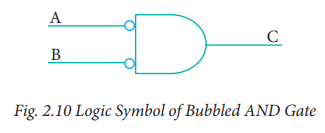
We refer this as bubbled AND gate. Let us analyse this logic circuit for all input possiblities.

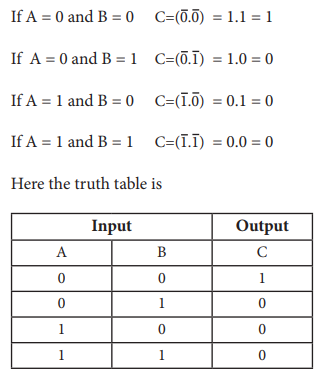
You can see that, a bubbled AND gate produces the same output as a NOR gate. So, You can replace each NOR gate by a bubbled AN D gate. In other words the circuits are interchangeable.

Therefore

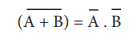
Which establishes the De Morgan's first theorem.

6.  NAND Gate

The NAND gate operates an AND gate followed by a NOT gate. It acts in the manner of the logical operation "AND" followed by inversion. The output is "false" if both inputs are "true", otherwise, the output is "true". In otherwords the output of the NAND gate is 0 if and only if both the inputs are 1, otherwise the output is 1. The logice circuit of NAND gate is

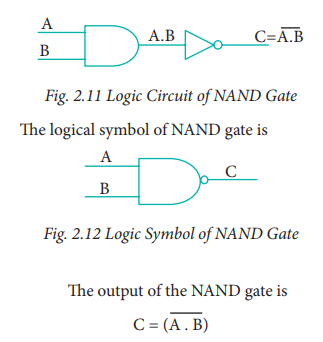
Read this as "C" equals NOT of A AND B" or "C" equals the complement of A AND B".

For example if both the inputs are 1

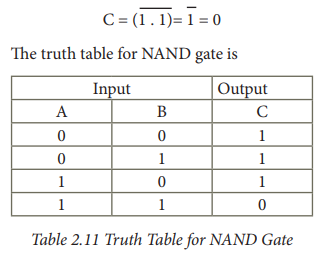
The truth table for NAND gate

7.  Bubbled OR Gate

The logic circuit of bubbled OR gate is

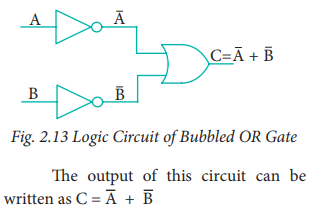
The above circuit can be redrawn as the bubbles on the input, where the bubbles represents the inversion.

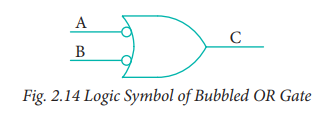
We refer this as bubbled OR gate. The truth table for the bubbled OR is

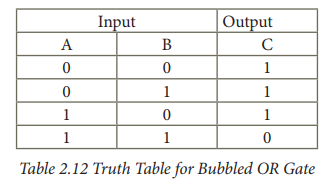
If we compare the truth tables of the bubbled OR gate with NAND gate, they are identical. So the circuits are interchangeable.

Therefore,

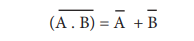
Which establishes the De Morgan's second theorem.

8.  XOR Gate

The XOR (exclusive - OR) gate acts in the same way as the logical "either/or." The output is "true" if either, but not both, of the inputs are "true". The output is "false" if both inputs are "false" or if both inputs are "true." Another way of looking at this circuit is to observe that the output is 1 if the inputs are different, but 0 if the inputs are the same. The logic circuit of XOR gate is

9.  XNOR Gate

The XNOR (exclusive - NOR) gate is a combination XOR gate followed by an inverter. Its output is "true" if the inputs are the same, and "false" if the inputs are different. In simple words, the output is 1 if the input are the same, otherwise the output is 0. The logic circuit of XNOR gate is

Using combination of logic gates, complex operations can be performed. In theory, there is no limit to the number of gates that can be arranged together in a single device. But in practice, there is a limit to the number of gates that can be packed into a given physical space. Arrays of logic gates are found in digital integrated circuits.